题目内容
1. 一列简谐横波沿x轴正方向传播,某时刻波形如图实线所示,经过时间△t=2.5s时波形如图虚线所示.求这列波传播的周期T和速率v.
一列简谐横波沿x轴正方向传播,某时刻波形如图实线所示,经过时间△t=2.5s时波形如图虚线所示.求这列波传播的周期T和速率v.
分析 根据波形图可知,波长为8m;波沿x轴正方向传播,传播的最短距离为2m,根据波的周期性:相隔整数倍周期的时间,波形相同,根据时间与周期关系的通项,求出周期,从而求出波速.
解答 解:由题意可知,波长为8m;设波的周期为T.若波沿x轴正方向传播,则有:
t=(n+$\frac{1}{4}$)T,
得:T=$\frac{4t}{4n+1}=\frac{10}{4n+1}$s (n=0,1,2,…)
根据$v=\frac{λ}{T}$得:波速v=0.8+3.2n (m/s),(n=0,1,2,…).
答:这列波传播的周期T为$\frac{4t}{4n+1}=\frac{10}{4n+1}$s (n=0,1,2,…),速率v为0.8+3.2n (m/s),(n=0,1,2,…).
点评 本题是波动图象中典型的问题,要根据波的周期性和双向性研究时间与周期的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12. 用同一光电管研究a、b两种单色光产生的光电效应,得到光电流I与光电管两极间所加电压U的关系如图.则这两种光的说法正确的有( )
用同一光电管研究a、b两种单色光产生的光电效应,得到光电流I与光电管两极间所加电压U的关系如图.则这两种光的说法正确的有( )
 用同一光电管研究a、b两种单色光产生的光电效应,得到光电流I与光电管两极间所加电压U的关系如图.则这两种光的说法正确的有( )
用同一光电管研究a、b两种单色光产生的光电效应,得到光电流I与光电管两极间所加电压U的关系如图.则这两种光的说法正确的有( )| A. | a光的光子频率大于b光的光子频率 | |
| B. | 用b光照射该光电管时逸出的光电子最大初动能大 | |
| C. | 单位时间内a光照射到光电管上的光子数少 | |
| D. | a光的遏止电压小于b光的遏止电压 |
13. 如图所示,自动卸货车始终静止在水平地面上,车厢在液压机的作用下可以改变与水平面间的倾角θ,用以卸下车厢中的货物.货物的质量为m,货物与车厢间的动摩擦因数为μ下列说法正确的是( )
如图所示,自动卸货车始终静止在水平地面上,车厢在液压机的作用下可以改变与水平面间的倾角θ,用以卸下车厢中的货物.货物的质量为m,货物与车厢间的动摩擦因数为μ下列说法正确的是( )
 如图所示,自动卸货车始终静止在水平地面上,车厢在液压机的作用下可以改变与水平面间的倾角θ,用以卸下车厢中的货物.货物的质量为m,货物与车厢间的动摩擦因数为μ下列说法正确的是( )
如图所示,自动卸货车始终静止在水平地面上,车厢在液压机的作用下可以改变与水平面间的倾角θ,用以卸下车厢中的货物.货物的质量为m,货物与车厢间的动摩擦因数为μ下列说法正确的是( )| A. | 当货物相对车厢静止时,货物与车厢间的摩擦力f=μmgcosθ | |
| B. | 当货物相对车厢静止时,货物与车厢间弹力FN=mgsinθ | |
| C. | 当货物相对车厢匀速下滑时,地面对汽车有向左的摩擦力 | |
| D. | 当货物相对车厢匀速下滑时,汽车对地面的压力等于货物和汽车的总重力 |
10.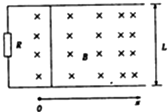 如图,两根电阻不计的平行光滑金属导轨水平放置,一端与电阻相连,导轨x>0一侧存在沿x方向均匀增大的稳恒磁场,其方向与导轨平面垂直,变化率k=0.5T/m,x=0处磁场的磁感应强度B0=0.5T,一根金属棒置于导轨上,并与导轨垂直.棒在外力作用下从x=0处以初速度v0=4m/s沿导轨向右运动,运动过程中电阻消耗的功率不变.则( )
如图,两根电阻不计的平行光滑金属导轨水平放置,一端与电阻相连,导轨x>0一侧存在沿x方向均匀增大的稳恒磁场,其方向与导轨平面垂直,变化率k=0.5T/m,x=0处磁场的磁感应强度B0=0.5T,一根金属棒置于导轨上,并与导轨垂直.棒在外力作用下从x=0处以初速度v0=4m/s沿导轨向右运动,运动过程中电阻消耗的功率不变.则( )
 如图,两根电阻不计的平行光滑金属导轨水平放置,一端与电阻相连,导轨x>0一侧存在沿x方向均匀增大的稳恒磁场,其方向与导轨平面垂直,变化率k=0.5T/m,x=0处磁场的磁感应强度B0=0.5T,一根金属棒置于导轨上,并与导轨垂直.棒在外力作用下从x=0处以初速度v0=4m/s沿导轨向右运动,运动过程中电阻消耗的功率不变.则( )
如图,两根电阻不计的平行光滑金属导轨水平放置,一端与电阻相连,导轨x>0一侧存在沿x方向均匀增大的稳恒磁场,其方向与导轨平面垂直,变化率k=0.5T/m,x=0处磁场的磁感应强度B0=0.5T,一根金属棒置于导轨上,并与导轨垂直.棒在外力作用下从x=0处以初速度v0=4m/s沿导轨向右运动,运动过程中电阻消耗的功率不变.则( )| A. | 金属棒在运动过程中产生的电动势不变 | |
| B. | 金属棒在运动过程中产生的安培力大小不变 | |
| C. | 金属棒在x=3m处的速度为2m/s | |
| D. | 金属棒在x=3m处的速度为1m/s |
11.下列关于力对物体做功的说法中正确的是( )
| A. | 摩擦力对物体做功的多少与路径有关 | |
| B. | 合力不做功,物体必定做匀速直线运动 | |
| C. | 在相同时间内作用力与反作用力做功绝对值一定相等,一正一负 | |
| D. | 一对作用力和反作用力可能其中一个力做功,而另一个力不做功 |
 如图所示,半径R、内径很小的光滑半圆管竖直放置,两个质量均为m的小球A、B以不同速度进入管内,A通过最高点C时,对管的上壁压力为3mg,B通过最高点C时,对管的下壁压力为0.75mg,求AB两球落地点间的距离.
如图所示,半径R、内径很小的光滑半圆管竖直放置,两个质量均为m的小球A、B以不同速度进入管内,A通过最高点C时,对管的上壁压力为3mg,B通过最高点C时,对管的下壁压力为0.75mg,求AB两球落地点间的距离.