题目内容
14. 如图所示,水平传送带BC左端与光滑水平面AB相连,右端与光滑曲面CD相连,一轻质弹簧的左端与固定的竖直挡板相连.现用一木块(可视为质点)将弹簧压缩至O点后静止释放,木块运动至光滑曲面后滑回,已知木块质量m=0.1kg,木块脱离弹簧时的速度v0=3m/s,传送带长度l=3m,若传送带静止,木块第一次滑回后静止在BC的中点,g取10m/s2,不计空气阻力.
如图所示,水平传送带BC左端与光滑水平面AB相连,右端与光滑曲面CD相连,一轻质弹簧的左端与固定的竖直挡板相连.现用一木块(可视为质点)将弹簧压缩至O点后静止释放,木块运动至光滑曲面后滑回,已知木块质量m=0.1kg,木块脱离弹簧时的速度v0=3m/s,传送带长度l=3m,若传送带静止,木块第一次滑回后静止在BC的中点,g取10m/s2,不计空气阻力.(1)求木块在O点时,弹簧的弹性势能.
(2)求传送带与木块间的动摩擦因数.
(3)若传送带顺时针转动,木块第一次滑回后恰好能滑至B点,试求木块第一次由B向C运动过程中摩擦力对木块做的功.
分析 (1)根据动能定理或能量守恒定律即可求解;
(2)对木块全过程应用能定理即可求解;
(3)通过分析存在两种情况,一种是一直匀减速到C,一种是先减速到传送带速度再匀速到C,然后再根据位移速度关系即可求解.
解答 解:(1)对木块由动能定理可得:Ep=$\frac{1}{2}$mv02-0,
解得Ep=$\frac{1}{2}×0.1×{3}^{2}$=0.45J;
(2)对木块从B到BC中点过程由动能定理可得:-μmg(l+$\frac{l}{2}$)=0-$\frac{1}{2}$mv${\;}_{0}^{2}$,
解得μ=0.1;
(3)根据题意木块从B滑到C时存在两种情况,一种是木块一直减速滑到C点,一种是先减到传送带速度然后与传送带一起匀速到C点:
第一种情况:设木块第一次到达C点时速度为v,应有:v2-v${\;}_{0}^{2}$=-2μgl
从C返回到B时应有:0-v2=-2μgl
比较可知无解,即第一种情况不存在;
第二种情况:设传送带的速度为v,从B到C时应有:v2-v${\;}_{0}^{2}$=-2μgx,其中x是木块匀减速发生的位移,
从C返回到B时应有:0-v2=-2μgl
联立以上两式解得x=$\frac{l}{2}$m,即说明木块正好滑到B、C的中点时正好与传送带速度相同;
所以木块第一次有B向C运动时先减速再匀速;
由上面分析可知,从B向C运动过程中摩擦力做的功为Wf1=-μmgx=-0.1×0.1×10×1.5J=-0.15J
答:(1)弹簧的弹性势能为0.45J;
(2)传送带与木块间的动摩擦因数为0.1;
(3)木块第一次有B向C运动过程是先减速后匀速,摩擦力做的功为-0.15J.
点评 应明确:①涉及到“动能、势能”、速度大小等与时间无关的动力学问题应用动能定理求解较简便;②有关传送带问题,注意物理过程分析,然后再根据相应的规律列式求解.

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案| A. | 0.1 m/s | B. | 0.5 m/s | C. | 1 m/s | D. | 2 m/ |

| A. | 只有A球和C球的振动周期相同 | B. | C球的振幅比B球的振幅小 | ||
| C. | C球的振幅比B球的振幅大 | D. | A球、B球、C球振动周期相同 |
 如图所示,从倾角为θ的足够长的斜面顶端P点以速度υ0抛出一个小球,落在斜面上Q点,小球落在斜面上的速度与斜面的夹角为α,若把初速度变成2υ0,下列说法正确的是( )
如图所示,从倾角为θ的足够长的斜面顶端P点以速度υ0抛出一个小球,落在斜面上Q点,小球落在斜面上的速度与斜面的夹角为α,若把初速度变成2υ0,下列说法正确的是( )| A. | 由于抛出点不变,空中运动时间不变 | |
| B. | 由于水平速度变大,α角将变小 | |
| C. | 水平位移将大于原来的2倍,PQ也将大于原来的2倍 | |
| D. | 夹角α与初速度大小无关 |
 如图,半径为R的光滑半圆形轨道ABC在竖直平面内,与水平轨道CD相切于C点,D端有一被锁定的轻质压缩弹簧,弹簧左端连接在固定的挡板上,弹簧右端Q到C点的距离为2R.质量为m的滑块(视为质点)从轨道上的P点由静止滑下,刚好能运动到Q点,并能触发弹簧解除锁定,然后滑块被弹回,且刚好能通过圆轨道的最高点A.已知∠POC=60°,求:
如图,半径为R的光滑半圆形轨道ABC在竖直平面内,与水平轨道CD相切于C点,D端有一被锁定的轻质压缩弹簧,弹簧左端连接在固定的挡板上,弹簧右端Q到C点的距离为2R.质量为m的滑块(视为质点)从轨道上的P点由静止滑下,刚好能运动到Q点,并能触发弹簧解除锁定,然后滑块被弹回,且刚好能通过圆轨道的最高点A.已知∠POC=60°,求:
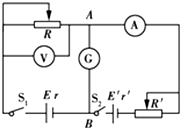 采用伏安法测量电源电动势E和内阻r时,由于电表因素带来了实验的系统误差.某研究性学习小组对此实验进行改进,设计出如图所示的测量电源电动势E和内电阻r的电路,E′是辅助电源,A、B两点间有一灵敏电流计G.
采用伏安法测量电源电动势E和内阻r时,由于电表因素带来了实验的系统误差.某研究性学习小组对此实验进行改进,设计出如图所示的测量电源电动势E和内电阻r的电路,E′是辅助电源,A、B两点间有一灵敏电流计G.