��Ŀ����
20�� �ҹ��ġ�����һ�š������ǵ���ͬ�����ǣ���Ϊ�е�������ṩ����ͨѶ����ͼΪ������һ�š�����a�����ƽ���ڵĵ������b�������λ�ù�ϵʾ��ͼ��OΪ���ģ������������a��b���ŽǷֱ�Ϊ��1�ͦ�2����2ͼ��δ�����������a�Ĺ���뾶��b��4������֪����a��b�Ƶ���ͬ�����У�����a������ΪT�������й��������ڵ�����ڵ�������b���������aͨѶ��ä�������Ǽ��ͨѶ�ź���Ϊ��ֱ�ߴ������źŴ���ʱ��ɺ��ԣ����з�����ȷ���ǣ�������
�ҹ��ġ�����һ�š������ǵ���ͬ�����ǣ���Ϊ�е�������ṩ����ͨѶ����ͼΪ������һ�š�����a�����ƽ���ڵĵ������b�������λ�ù�ϵʾ��ͼ��OΪ���ģ������������a��b���ŽǷֱ�Ϊ��1�ͦ�2����2ͼ��δ�����������a�Ĺ���뾶��b��4������֪����a��b�Ƶ���ͬ�����У�����a������ΪT�������й��������ڵ�����ڵ�������b���������aͨѶ��ä�������Ǽ��ͨѶ�ź���Ϊ��ֱ�ߴ������źŴ���ʱ��ɺ��ԣ����з�����ȷ���ǣ�������| A�� | ����a��b���ٶ�֮��Ϊ2��1 | |
| B�� | ����b������Ϊ$\frac{T}{8}$ | |
| C�� | ����bÿ����ä�����е�ʱ��$\frac{{��}_{1}+{��}_{2}}{14��}$T | |
| D�� | ����bÿ����ä�����е�ʱ��$\frac{{��}_{1}+{��}_{2}}{16��}$T |
���� �����������ṩ����������ʽ�������a��b���ٶ�֮���Լ�����b�����ڣ����Ǽ��ͨѶ�ź���Ϊ��ֱ�ߴ������ɼ��ι�ϵ�õ�����b��ä����������Ե����ڵ�����Žǣ��������ä�����е�ʱ�䣮
��� 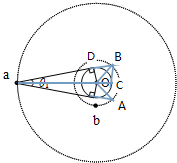 �⣺A��������a��b�Ĺ���뾶�ֱ�Ϊr1��r2������뾶ΪR������$G\frac{Mm}{{r}^{2}}=m\frac{{v}^{2}}{r}$�ã�$v=\sqrt{\frac{GM}{r}}$������a��b���ٶ�֮��Ϊ1��2����A����
�⣺A��������a��b�Ĺ���뾶�ֱ�Ϊr1��r2������뾶ΪR������$G\frac{Mm}{{r}^{2}}=m\frac{{v}^{2}}{r}$�ã�$v=\sqrt{\frac{GM}{r}}$������a��b���ٶ�֮��Ϊ1��2����A����
B����$G\frac{Mm}{{r}^{2}}=m\frac{{4��}^{2}r}{{T}^{2}}$�ɵ� T=2��$\sqrt{\frac{{r}^{3}}{GM}}$���ɵ� r1=4r2���������b�ǵ�����Ϊ$\frac{T}{8}$����B��ȷ��
CD����ͼ��A��B������ä��������Եλ�ã��ɼ���֪ʶ�ɵá�AOB=��1+��2���� ��$\frac{2��}{\frac{t}{8}}-\frac{2��}{T}$��t=��AOB=��1+��2��
��ã�bÿ����ä�����е�ʱ��Ϊ t=$\frac{{��}_{1}+{��}_{2}}{14��}$T����C��ȷ��D����
��ѡ��BC
���� �����Ҫ������������Ļ���˼·�����������ṩ������������Ҫ���ǻ���ʾ��ͼ�����ü���֪ʶ���

��ϰ��ϵ�д�
 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�
�����Ŀ
8�� �ڵ糡�е�A��B�����ֱ����벻ͬ����̽���q���õ���̽������ܵĵ糡���������仯�Ĺ�ϵ��ͼ��ʾ��������
�ڵ糡�е�A��B�����ֱ����벻ͬ����̽���q���õ���̽������ܵĵ糡���������仯�Ĺ�ϵ��ͼ��ʾ��������
 �ڵ糡�е�A��B�����ֱ����벻ͬ����̽���q���õ���̽������ܵĵ糡���������仯�Ĺ�ϵ��ͼ��ʾ��������
�ڵ糡�е�A��B�����ֱ����벻ͬ����̽���q���õ���̽������ܵĵ糡���������仯�Ĺ�ϵ��ͼ��ʾ��������| A�� | EA��EB | B�� | EA��EB | ||
| C�� | EA=EB | D�� | �����ж�EA��EB�Ĵ�С |
11�� ��ͼ��ʾ��������ȫ��ͬ�Ľ�����a��b�������ǹ̶��ھ�Ե֧���ϣ������ļ�ľ���lΪ��뾶��3������ʹ���Ǵ��ϵ������ֵ�ɣ��������ΪQ��a��b����֮��Ŀ�����F1��������Ϊ��Ե�������������ΪQ���ҵ�ɾ��ȷֲ��������ϣ���ʱa��b����֮��Ŀ�����F2��������
��ͼ��ʾ��������ȫ��ͬ�Ľ�����a��b�������ǹ̶��ھ�Ե֧���ϣ������ļ�ľ���lΪ��뾶��3������ʹ���Ǵ��ϵ������ֵ�ɣ��������ΪQ��a��b����֮��Ŀ�����F1��������Ϊ��Ե�������������ΪQ���ҵ�ɾ��ȷֲ��������ϣ���ʱa��b����֮��Ŀ�����F2��������
 ��ͼ��ʾ��������ȫ��ͬ�Ľ�����a��b�������ǹ̶��ھ�Ե֧���ϣ������ļ�ľ���lΪ��뾶��3������ʹ���Ǵ��ϵ������ֵ�ɣ��������ΪQ��a��b����֮��Ŀ�����F1��������Ϊ��Ե�������������ΪQ���ҵ�ɾ��ȷֲ��������ϣ���ʱa��b����֮��Ŀ�����F2��������
��ͼ��ʾ��������ȫ��ͬ�Ľ�����a��b�������ǹ̶��ھ�Ե֧���ϣ������ļ�ľ���lΪ��뾶��3������ʹ���Ǵ��ϵ������ֵ�ɣ��������ΪQ��a��b����֮��Ŀ�����F1��������Ϊ��Ե�������������ΪQ���ҵ�ɾ��ȷֲ��������ϣ���ʱa��b����֮��Ŀ�����F2��������| A�� | F1=k$\frac{{Q}^{2}}{{l}^{2}}$��F2=k$\frac{{Q}^{2}}{{l}^{2}}$ | B�� | F1��k$\frac{{Q}^{2}}{{l}^{2}}$��F2��k$\frac{{Q}^{2}}{{l}^{2}}$ | ||
| C�� | F1��k$\frac{{Q}^{2}}{{l}^{2}}$��F2=k$\frac{{Q}^{2}}{{l}^{2}}$ | D�� | F1=k$\frac{{Q}^{2}}{{l}^{2}}$��F2��k$\frac{{Q}^{2}}{{l}^{2}}$ |
5��һ�ʵ���x�����˶�����ʱ��λ���������±���������ӵ�2�������3��ĩ����λ�ƵĴ�СΪx1��ƽ���ٶ�Ϊv1�ڵ�4���ڷ���λ�ƴ�СΪx2��ƽ���ٶ�Ϊv2������
| t��s��ĩ | 0 | 1 | 2 | 3 | 4 |
| x ��m�� | 0 | 4 | 8 | -1 | -4 |
| A�� | x1��x2�������෴ | B�� | x1��x2��������ͬ | C�� | v1��v2��������ͬ | D�� | v1��v2�������෴ |
12��Ǧ���صĵ綯��Ϊ2V�����ʾ��������
| A�� | ��·��ÿͨ��1C���������Դ��0.5J�Ļ�ѧ��ת��Ϊ���� | |
| B�� | ����������ĵ�ѹΪ2V | |
| C�� | ������1s�ڽ�2J�Ļ�ѧ��ת��ɵ��� | |
| D�� | ���ؽ���ѧ��ת��Ϊ���ܵı����һ�ڸɵ�أ��綯��Ϊ1.5V���Ĵ� |
10�������ĸ�ͼ��ʾ����������ֱ���˶���ͼ���ǣ�������
| A�� |  | B�� |  | C�� |  | D�� |  |
 ���������������ɿ��Բ������������
���������������ɿ��Բ������������ ��ͼ��ʾ������A��B��ͬһƽ�����Ƶ���������Բ���˶�����������Ϊ0����OA��0B��н�Ϊ��ʱ��A��O��A��B��ľ�����ȣ���֪����A����������ΪT��������B���������ڣ�
��ͼ��ʾ������A��B��ͬһƽ�����Ƶ���������Բ���˶�����������Ϊ0����OA��0B��н�Ϊ��ʱ��A��O��A��B��ľ�����ȣ���֪����A����������ΪT��������B���������ڣ�