题目内容
8.已知月球探测器在距月球表面高为h的轨道围绕月球做匀速圆周运动的周期为T.月球视为半径为R的均匀球体,引力常量为G,求:(1)月球的质量;
(2)月球的第一宇宙速度v.
分析 (1)根据万有引力提供向心力求月球质量
(2)根据万有引力等于向心力和重力等于万有引力联立求第一宇宙速度
解答 解:(1)根据万有引力提供向心力
$G\frac{Mm}{(R+h)_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}(R+h)$
解得$M=\frac{4{π}_{\;}^{2}(R+h)_{\;}^{3}}{G{T}_{\;}^{2}}$
(2)月球的近地卫星的速度等于第一宇宙的速度
G$\frac{Mm}{{R}_{\;}^{2}}=m\frac{{v}_{\;}^{2}}{R}$
解得$v=\sqrt{\frac{GM}{R}}=\sqrt{\frac{4{π}_{\;}^{2}(R+h)_{\;}^{3}}{R{T}_{\;}^{2}}}$
答:(1)月球的质量$\frac{4{π}_{\;}^{2}(R+h)_{\;}^{3}}{G{T}_{\;}^{2}}$;
(2)月球的第一宇宙速度v为$\sqrt{\frac{4{π}_{\;}^{2}(R+h)_{\;}^{3}}{R{T}_{\;}^{2}}}$
点评 解决本题的关键掌握万有引力定律的两个重要理论:1、万有引力等于重力,2、万有引力提供向心力,并能灵活运用.

练习册系列答案
相关题目
19.关于万有引力定律F=G$\frac{{m}_{1}{m}_{2}}{{r}^{2}}$,下列说法正确的是( )
| A. | 当两物体的距离r趋近于零时,物体间的万有引力F将趋近于无穷大 | |
| B. | 万有引力定律是开普勒发现的 | |
| C. | 引力常量G是英国物理学家卡文迪许测量得出的 | |
| D. | 两个质量分布均匀的分离球体之间的相互作用力可以用F=G$\frac{{m}_{1}{m}_{2}}{{r}^{2}}$来计算,r是两个球心之间的距离 |
3.下列关于万有引力定律的说法,正确的是( )
| A. | 万有引力定律是卡文迪许发现的 | |
| B. | 自然界中的任何两个物体之间都存在万有引力 | |
| C. | 万有引力定律公式F=G$\frac{Mm}{r^2}$中的G是一个比例常数,是没有单位的 | |
| D. | 万有引力定律公式F=G$\frac{Mm}{r^2}$表明当r趋近于零时,万有引力为无穷大 |
13.甲星球绕乙星球做圆周运动的半径为r1,周期为T1;丙星球绕甲星球做圆周运动的半径为r2,周期为T2.引力常量为G,不计周围其他天体的影响,则根据给定条件( )
| A. | 能得到表达式$\frac{{{r}_{1}}^{3}}{{{T}_{1}}^{2}}$=$\frac{{{r}_{2}}^{3}}{{{T}_{2}}^{2}}$ | |
| B. | 能求出甲星球的质量 | |
| C. | 能求出甲星球与乙星球之间的万有引力 | |
| D. | 能求出甲星球与丙星球之间的万有引力 |
20.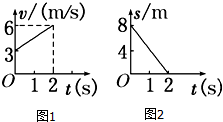 质量为2kg的质点在x-y平面上做曲线运动,在x方向的速度图象和y方向的位移图象如图所示,下列说法正确的是( )
质量为2kg的质点在x-y平面上做曲线运动,在x方向的速度图象和y方向的位移图象如图所示,下列说法正确的是( )
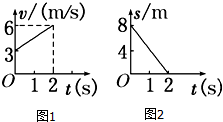 质量为2kg的质点在x-y平面上做曲线运动,在x方向的速度图象和y方向的位移图象如图所示,下列说法正确的是( )
质量为2kg的质点在x-y平面上做曲线运动,在x方向的速度图象和y方向的位移图象如图所示,下列说法正确的是( )| A. | 质点的初速度为3 m/s | |
| B. | 2s末质点速度大小为6 m/s | |
| C. | 质点做曲线运动的加速度为1.5m/s2 | |
| D. | 质点初速度的方向与合外力方向垂直 |
17.关于黑体及黑体辐射下列说法正确的是( )
| A. | 黑体是真实存在的 | |
| B. | 黑体辐射电磁波的强度与温度有关 | |
| C. | 随着温度升高黑体辐射中的有些成分会增强,有些成分会减弱 | |
| D. | 随着温度升高黑体辐射中强度最强的那一部分始终不变 |
 在“研究感应电流产生的条件”实验中:
在“研究感应电流产生的条件”实验中: