题目内容
8.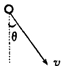 在匀强电场中,将质量为m,带电量为q的小球由静止释放,带电小球的运动轨迹为一直线,该直线与竖直方向的夹角为θ,如图所示,则电场强度的大小为( )
在匀强电场中,将质量为m,带电量为q的小球由静止释放,带电小球的运动轨迹为一直线,该直线与竖直方向的夹角为θ,如图所示,则电场强度的大小为( )| A. | 有唯一值$\frac{mgtanθ}{q}$ | B. | 最小值是$\frac{mgsinθ}{q}$ | C. | 最大值$\frac{mgtanθ}{q}$ | D. | $\frac{mg}{q}$ |
分析 带电小球在电场中受到重力和电场力,从O点自由释放,其运动轨迹为直线,小球所受的合力方向沿此直线方向,运用三角定则分析什么情况下场强大小最小,再求出最小值.
解答  解:带电小球的运动轨迹为直线,在电场中受到重力mg和电场力F,其合力必定沿此直线向下,根据三角形定则作出合力,由图看出,符合条件的电场强度有多个;而当电场力F与此直线垂直时,电场力F最小,场强最小,则有F=qEmin=mgsinθ,得到场强的最小值为 Emin=$\frac{mgsinθ}{q}$,由图可知,最大值无法求出.故ACD错误,B正确;
解:带电小球的运动轨迹为直线,在电场中受到重力mg和电场力F,其合力必定沿此直线向下,根据三角形定则作出合力,由图看出,符合条件的电场强度有多个;而当电场力F与此直线垂直时,电场力F最小,场强最小,则有F=qEmin=mgsinθ,得到场强的最小值为 Emin=$\frac{mgsinθ}{q}$,由图可知,最大值无法求出.故ACD错误,B正确;
故选:B.
点评 本题考查小球在电场和重力场中的平衡问题,要注意将电场力作为普通力进行分析即可,采用作图法分析场强取得最小值的条件,也可以采用函数法分析电场力与θ的关系,确定最小值的条件.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
19.关于探究小车速度随时间变化的规律的实验,下列说法中正确的是( )
| A. | 打点计时器应接交流电源 | |
| B. | 应先释放纸带,后接通电源打点 | |
| C. | 需使用秒表测出小车运动的时间 | |
| D. | 只要测出纸带上任意两点迹间的距离,就可求出小车运动的加速度 |
16.关于力,下列说法正确的是( )
| A. | 有受力物体就一定有施力物体 | |
| B. | 只有相互接触的物体才能产生力 | |
| C. | 一个物体是施力物体,但不是受力物体 | |
| D. | 力有时能脱离物体而独立存在 |
3. 钓鱼岛自古就是我国固有的领土,它到温州的直线距离为356km.若某天我国海监船为维护我国对钓鱼岛的主权,早上8:00从温州出发去钓鱼岛巡航,航行了480km,历时8时20分到达钓鱼岛.下列说法中正确的是( )
钓鱼岛自古就是我国固有的领土,它到温州的直线距离为356km.若某天我国海监船为维护我国对钓鱼岛的主权,早上8:00从温州出发去钓鱼岛巡航,航行了480km,历时8时20分到达钓鱼岛.下列说法中正确的是( )
 钓鱼岛自古就是我国固有的领土,它到温州的直线距离为356km.若某天我国海监船为维护我国对钓鱼岛的主权,早上8:00从温州出发去钓鱼岛巡航,航行了480km,历时8时20分到达钓鱼岛.下列说法中正确的是( )
钓鱼岛自古就是我国固有的领土,它到温州的直线距离为356km.若某天我国海监船为维护我国对钓鱼岛的主权,早上8:00从温州出发去钓鱼岛巡航,航行了480km,历时8时20分到达钓鱼岛.下列说法中正确的是( )| A. | 8:00是指时间间隔 | |
| B. | 8时20分是指时间间隔 | |
| C. | 8时20分是指时刻 | |
| D. | 该海监船位移大小为480 km,路程为356 km |
13.关于静电,以下说法中正确的是( )
| A. | 干燥天气里脱化纤衣物时常常会看到火花,听到噼啪声,这是火花放电现象 | |
| B. | 室内栽花种草可有效防止静电 | |
| C. | 高压输电导线表面要很光滑,主要是为了美观 | |
| D. | 油罐车尾装一条拖地铁链,有利于消除静电 |
17. 如图所示,人在岸上拉船,已知船的质量为m,水的阻力恒为f,当轻绳与水平面的夹角为θ时,船的速度为v,此时人的拉力大小为F,则( )
如图所示,人在岸上拉船,已知船的质量为m,水的阻力恒为f,当轻绳与水平面的夹角为θ时,船的速度为v,此时人的拉力大小为F,则( )
 如图所示,人在岸上拉船,已知船的质量为m,水的阻力恒为f,当轻绳与水平面的夹角为θ时,船的速度为v,此时人的拉力大小为F,则( )
如图所示,人在岸上拉船,已知船的质量为m,水的阻力恒为f,当轻绳与水平面的夹角为θ时,船的速度为v,此时人的拉力大小为F,则( )| A. | 人拉绳行走的速度为vsinθ | B. | 人拉绳行走的速度为$\frac{v}{cosθ}$ | ||
| C. | 人拉绳行走的速度为vcosθ | D. | 人拉绳行走的速度为vtanθ |
 如图所示,在区域I和区域Ⅱ内分别存在匀强电场,电场强度大小均为E,但方向不同.在区域I内场强方向沿y轴正方向,区域Ⅱ内场强方向未标明,两处电场都处在xoy平面内.一质量为m,电量为q的正粒子从坐标原点O以某一初速度沿x轴正方向射入电场区域I,从P点进入电场区域Ⅱ,到达Ⅱ区域右边界Q处时速度恰好为零.P点的坐标为(L,$\frac{L}{2}$).不计粒子所受重力,求:
如图所示,在区域I和区域Ⅱ内分别存在匀强电场,电场强度大小均为E,但方向不同.在区域I内场强方向沿y轴正方向,区域Ⅱ内场强方向未标明,两处电场都处在xoy平面内.一质量为m,电量为q的正粒子从坐标原点O以某一初速度沿x轴正方向射入电场区域I,从P点进入电场区域Ⅱ,到达Ⅱ区域右边界Q处时速度恰好为零.P点的坐标为(L,$\frac{L}{2}$).不计粒子所受重力,求: 如图所示,甲、乙、丙三辆车行驶在平直公路上,车速分别为5m/s、8m/s、10m/s.当甲、乙、丙三车依次相距6m时,乙驾驶员发现甲车开始以1m/s2的加速度做匀减速运动,于是乙也立即做匀减速运动,丙车亦同样处理,直到三车都停下来时均未发生撞车事故.
如图所示,甲、乙、丙三辆车行驶在平直公路上,车速分别为5m/s、8m/s、10m/s.当甲、乙、丙三车依次相距6m时,乙驾驶员发现甲车开始以1m/s2的加速度做匀减速运动,于是乙也立即做匀减速运动,丙车亦同样处理,直到三车都停下来时均未发生撞车事故.