题目内容
18.质点从A到B沿直线运动,已知其初速度为零.从A到中间某一点C的加速度为a1,方向与运动方向相同,从C到B加速度大小为a2,方向与运动方向相反,到达B点时速度恰好为零,AB=L,求(1)大体画出速度-时间图象;
(2)求AC:BC;
(3)从A到B的平均速度$\overline v$;
(4)通过C点时的即时速度vC.
分析 (1)根据运动的特点即可画出v-t图;
(2)根据位移速度公式即可求出位移之间的关系;
(3)根据平均速度的公式求出全程的平均速度;
(4)设C点的速度为v,根据匀变速直线运动的速度位移公式,抓住总位移为L,求出C点的瞬时速度.
解答 解:(1)由题可知,质点先做加速运动,后做减速运动,末速度等于0,所以其v-t图象大体如图:
(2)因为vc2=2a1xAC,vc2=2a2xCB,则xAC:xCB=a2:a1.
(3)(4)设C点的速度为vC,有$\frac{{{v}_{C}}^{2}}{2{a}_{1}}+\frac{{{v}_{C}}^{2}}{2{a}_{2}}=L$,解得:vC=$\sqrt{\frac{{2a}_{1}{a}_{2}L}{{a}_{1}+{a}_{2}}}$,
根据平均速度的公式有:$\frac{{v}_{C}}{2}{t}_{1}+\frac{{v}_{C}}{2}{t}_{2}=L$,则平均速度为:$\overline{{v}_{AB}}=\frac{L}{{t}_{1}+{t}_{2}}=\frac{{v}_{C}}{2}=\frac{\sqrt{\frac{2{a}_{1}{a}_{2}L}{{a}_{1}+{a}_{2}}}}{2}$.
答:(1)画出速度-时间图象如图;
(2)AC:BC的比值等于a2:a1;
(3)从A到B的平均速度是$\frac{\sqrt{\frac{2{a}_{1}{a}_{2}L}{{a}_{1}+{a}_{2}}}}{2}$;
(4)通过C点时的即时速度是$\sqrt{\frac{{2a}_{1}{a}_{2}L}{{a}_{1}+{a}_{2}}}$.
点评 解决本题的关键掌握匀变速直线运动的公式和推论,并能灵活运用,该题也可利用图象进行解答.

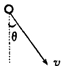 在匀强电场中,将质量为m,带电量为q的小球由静止释放,带电小球的运动轨迹为一直线,该直线与竖直方向的夹角为θ,如图所示,则电场强度的大小为( )
在匀强电场中,将质量为m,带电量为q的小球由静止释放,带电小球的运动轨迹为一直线,该直线与竖直方向的夹角为θ,如图所示,则电场强度的大小为( )| A. | 有唯一值$\frac{mgtanθ}{q}$ | B. | 最小值是$\frac{mgsinθ}{q}$ | C. | 最大值$\frac{mgtanθ}{q}$ | D. | $\frac{mg}{q}$ |
 一种比飞机还要快的旅行工具即将诞生,称为“第五类交通方式”,它就是“Hyperloop(超级高铁)”.据英国《每日邮报》2016年7月6日报道,Hyperloop One公司计划,将在欧洲建成世界首架规模完备的“超级高铁”(Hyperloop),连接芬兰首都赫尔辛基和瑞典首都斯德哥尔摩,速度可达每小时700英里(约合1126公里/时).如果乘坐Hyperloop从赫尔辛基到斯德哥尔摩,600公里的路程需要40分钟,Hyperloop先匀加速,达到最大速度1200km/h后匀速运动,快进站时再匀减速运动,且加速与减速的加速度大小相等,则下列关于Hyperloop的说法正确的是( )
一种比飞机还要快的旅行工具即将诞生,称为“第五类交通方式”,它就是“Hyperloop(超级高铁)”.据英国《每日邮报》2016年7月6日报道,Hyperloop One公司计划,将在欧洲建成世界首架规模完备的“超级高铁”(Hyperloop),连接芬兰首都赫尔辛基和瑞典首都斯德哥尔摩,速度可达每小时700英里(约合1126公里/时).如果乘坐Hyperloop从赫尔辛基到斯德哥尔摩,600公里的路程需要40分钟,Hyperloop先匀加速,达到最大速度1200km/h后匀速运动,快进站时再匀减速运动,且加速与减速的加速度大小相等,则下列关于Hyperloop的说法正确的是( )| A. | 加速与减速的时间不一定相等 | |
| B. | 加速时间为10分钟 | |
| C. | 加速时加速度大小为0.56 m/s2 | |
| D. | 如果加速度大小为10 m/s2,题中所述运动最短需要32分钟 |
 如图示(俯视),原来静止在光滑水平桌面上的物体,现在受到一个水平向东的力F1的作用,若要使物体的合力沿东偏北30°方向,则必须同时对物体施加另一个水平作用力F2,那么F2最小值为( )
如图示(俯视),原来静止在光滑水平桌面上的物体,现在受到一个水平向东的力F1的作用,若要使物体的合力沿东偏北30°方向,则必须同时对物体施加另一个水平作用力F2,那么F2最小值为( )| A. | $\frac{1}{2}{F_1}$ | B. | $\frac{{\sqrt{3}}}{3}{F_1}$ | C. | $\frac{{\sqrt{3}}}{2}{F_1}$ | D. | $\sqrt{3}{F_1}$ |
 如图所示,单匝正方形线圈在外力作用下以速度υ向右匀速进入匀强磁场,第二次又以速度2υ匀速进入同一匀强磁场.第二次进入磁场与第一次进入比较( )
如图所示,单匝正方形线圈在外力作用下以速度υ向右匀速进入匀强磁场,第二次又以速度2υ匀速进入同一匀强磁场.第二次进入磁场与第一次进入比较( )| A. | 回路的电流I2:I1=2:1 | B. | 外力的功率P2:P1=4:1 | ||
| C. | 产生的热量Q2:Q1=4:1 | D. | 回路中流过的电量q2:q1=2:1 |





 如图所示,一质量为m的木块靠在竖直粗糙墙壁上,木块与墙的滑动摩擦系数为μ,当受到水平力F的作用时,使木块静止,此时木块受到的摩擦力大小为mg,方向向上,当撤去F,木块沿墙壁下滑时,木块受摩擦力大小为零.
如图所示,一质量为m的木块靠在竖直粗糙墙壁上,木块与墙的滑动摩擦系数为μ,当受到水平力F的作用时,使木块静止,此时木块受到的摩擦力大小为mg,方向向上,当撤去F,木块沿墙壁下滑时,木块受摩擦力大小为零. 如图所示,一个质点沿两个半径为R的半圆弧由A运动到C,规定向右方向为正方向,在此过程中,它的位移大小是4R和路程为2πR.
如图所示,一个质点沿两个半径为R的半圆弧由A运动到C,规定向右方向为正方向,在此过程中,它的位移大小是4R和路程为2πR.