题目内容
3．如图所示的装置，通过动滑轮和定滑轮悬挂重均为G的两个物体，图中虚线保持水平，则θ角为（ ）
| A． | 45° | B． | 30° | C． | 60° | D． | 75° |
分析 先对右边物体受力分析，根据平衡条件得到绳子的拉力T；再对滑轮和左侧物体整体受力分析，受重力和两边绳子的拉力而平衡．
解答 解：先对右侧物体受力分析，受拉力和重力而平衡，故T=G；
再对左侧物体和滑轮整体分析，受两个绳子的拉力和重力，三个力的大小都等于G，根据平衡条件，三个力可以构成首尾相连的矢量三角形，故该三角形是等边三角形，故两个细线的拉力的夹角为120°，故θ角为30°；
故选：B
点评 本题是力平衡问题，关键正确的受力分析后根据平衡条件列式求解．
三力平衡的基本解题方法：
①力的合成、分解法：即分析物体的受力，把某两个力进行合成，将三力转化为二力，构成一对平衡力，二是把重力按实际效果进行分解，将三力转化为四力，构成两对平衡力．
②相似三角形法：利用矢量三角形与几何三角形相似的关系，建立方程求解力的方法．应用这种方法，往往能收到简捷的效果．
练习册系列答案
相关题目
13．
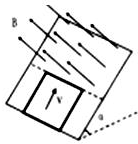如图所示，光滑斜面的上半部分有垂直于斜面向上的匀强磁场，边长为L的正方体导体线框以初速度v0开始沿斜面向上进入磁场，通过一段位移x后，又沿斜面返回出发点．若x≤L，则线框在斜面上运动的过程中，下列说法正确的是（ ）
如图所示，光滑斜面的上半部分有垂直于斜面向上的匀强磁场，边长为L的正方体导体线框以初速度v0开始沿斜面向上进入磁场，通过一段位移x后，又沿斜面返回出发点．若x≤L，则线框在斜面上运动的过程中，下列说法正确的是（ ）| A． | 线框上滑的时间比下滑的时间短 | |
| B． | 线框的加速度先增大再减小 | |
| C． | 上滑过程中通过线框截面的电荷量比下滑过程中的大 | |
| D． | 上滑过程中产生的焦耳热比下滑过程的多 |
14．
某电场的电场强度E随时间t变化规律的图象如图6所示．当t=0时，在该电场中由静止释放一个带电粒子，设带电粒子只受电场力作用，则下列说法中正确的是（ ）
某电场的电场强度E随时间t变化规律的图象如图6所示．当t=0时，在该电场中由静止释放一个带电粒子，设带电粒子只受电场力作用，则下列说法中正确的是（ ）| A． | 带电粒子将始终向同一个方向运动 | |
| B． | 带电粒子在0-3s内的初、末位置间的电势差为零 | |
| C． | 2s末带电粒子回到原出发点 | |
| D． | 0-2s内，电场力的总功不为零 |
11．电源与外电阻R连接成闭合回路，对于电源的路端电压U，下列说法正确的是（ ）
| A． | 因U=IR，则U 与R的大小成正比 | |
| B． | 因U=IR，则R=0时，必有U=0 | |
| C． | 流过电源的电流越大，路端电压U也越大 | |
| D． | 若外电路断开，回路中电流为0，路端电压也等于0 |
在研究匀变速直线运动的实验中，如图所示，为一次记录小车运动情况的纸带，图中A、B、C、D、E为相邻的记数点，相邻记数点间的时间间隔T=0.1s．
8．
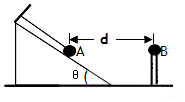如图所示，水平地面上固定一个光滑绝缘斜面，斜面与水平面的夹角为θ．一根轻质绝缘细线的一端固定在斜面顶端，另一端系有一个带电小球A，细线与斜面平行．小球A的质量为m、电量为q．小球A的右侧固定放置带等量同种电荷的小球B，两球心的高度相同、间距为d．静电力常量为k，重力加速度为g，两带电小球可视为点电荷．小球A静止在斜面上，则下列说法中正确的是（ ）
如图所示，水平地面上固定一个光滑绝缘斜面，斜面与水平面的夹角为θ．一根轻质绝缘细线的一端固定在斜面顶端，另一端系有一个带电小球A，细线与斜面平行．小球A的质量为m、电量为q．小球A的右侧固定放置带等量同种电荷的小球B，两球心的高度相同、间距为d．静电力常量为k，重力加速度为g，两带电小球可视为点电荷．小球A静止在斜面上，则下列说法中正确的是（ ）| A． | 小球A与B之间库仑力的大小为kq2/d | |
| B． | 当$\frac{q}{d}$=$\sqrt{\frac{mgsinθ}{k}}$时，细线上的拉力为0 | |
| C． | 当$\frac{q}{d}$=$\sqrt{\frac{mgtanθ}{k}}$时，细线上的拉力为0 | |
| D． | 当$\frac{q}{d}$=$\sqrt{\frac{mg}{ktanθ}}$时，斜面对小球A的支持力为0 |
15．
成都的二环高架一直是成都交通的大动脉，全长 28.3 公里，主线无红绿灯，有多座立交及匝道进行交通转换，记者乘出租车体验高架桥给人们出行带来的快捷．10 时30分，记者从二环路科华立交口出发，在 10 时 42分到达红牌楼路口，计价器显示 6.20 公里．记者注意到在高架上车速最高达达到 80km/h，下列说法正确的是（ ）
成都的二环高架一直是成都交通的大动脉，全长 28.3 公里，主线无红绿灯，有多座立交及匝道进行交通转换，记者乘出租车体验高架桥给人们出行带来的快捷．10 时30分，记者从二环路科华立交口出发，在 10 时 42分到达红牌楼路口，计价器显示 6.20 公里．记者注意到在高架上车速最高达达到 80km/h，下列说法正确的是（ ）| A． | 计价器上显示的公里数 6.2 表示位移 | |
| B． | 80 km/h 表示的是瞬时速率 | |
| C． | 全程的平均速率约为 30 km/h | |
| D． | 10 时 42 分是时间 |
如图所示，质量均匀分布的球重为G，用细绳将球挂在光滑的竖直墙壁上，绳与墙的夹角为α，其延长线过球心，求绳对球的拉力和墙对球的支持力．