题目内容
【题目】做功与路径无关的力场叫做势场，在这类场中可以引入“势”和“势能”的概念，场力做功可以量度势能的变化．例如重力场和电场．
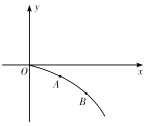
某势场的势
随
的分布可简化为如图所示的折线，图中
和
为已知量．一个质点在该势场中，仅在场力的作用下，在场中以
为中心，沿轴方向做周期性运动．已知质点的质点为
，受到的场力方向平行于轴，其势能可表示为
（
为不变量），动能与势能之和恒为
．
（
）求质点的最大速率
；
（
）求质点的运动区间；
（
）试论证质量在该势场中所受场力的大小不变，并求质点的运动周期．
【答案】（
）
；（
）
；（
）
【解析】（1）当物体经过x=0的位置时，电势为零，则电势能为零，动能和速度最大，则有：
解得：
（）如图所示：
设物体的运动区间为
，当物体运动到
处时，其势能最大，动能为零，则有：
，即
又因为
，
，又
，所以
即物体的运动区间为：
．
（3）由题意可知，场力的势能表示为
，则质点在场中的势能可表示为
因为
，所以可得
根据牛顿第二定律，质点加速度的大小为：
运动时间：
所以质点的运动周期：
练习册系列答案
相关题目
