题目内容
18. 如图所示,空间存在垂直于纸面的匀强磁场,在半径为a的圆形区域内部及外部,磁场方向相反,磁感应强度的大小均为B.一半径为b(b>a),电阻为R的圆形导线环放置在纸面内,其圆心与圆形区域的中心重合.当内、外磁场同时由B均匀地减小到零的过程中,通过导线截面的电量为( )
如图所示,空间存在垂直于纸面的匀强磁场,在半径为a的圆形区域内部及外部,磁场方向相反,磁感应强度的大小均为B.一半径为b(b>a),电阻为R的圆形导线环放置在纸面内,其圆心与圆形区域的中心重合.当内、外磁场同时由B均匀地减小到零的过程中,通过导线截面的电量为( )| A. | $\frac{πB|{b}^{2}-2{a}^{2}|}{R}$ | B. | $\frac{πB|{b}^{2}+2{a}^{2}|}{R}$ | C. | $\frac{πB|{b}^{2}-{a}^{2}|}{R}$ | D. | $\frac{πB|{b}^{2}+{a}^{2}|}{R}$ |
分析 产生的电荷量q=It,根据磁通量的变化率求平均感应电动势,从而表示出电流与时间的乘积表达式.
解答 解:初始状态导线环中的磁通量为:
Φ1=(πb2-πa2)B-πa2B
末状态导线环中的磁通量为:
Φ2=0
其磁通量的变化量:
|△Φ|=|Φ2-Φ1|=|(πb2-2πa2)B|
产生的电荷量:
$q=It=\frac{△Φ}{△tR}△t=\frac{△Φ}{R}=\frac{|(π{b}_{\;}^{2}-2π{a}_{\;}^{2})B|}{R}$=$\frac{πB|{b}_{\;}^{2}-2{a}_{\;}^{2}|}{R}$
故选:A
点评 不同考查了平均感应电动势的求法,注意根据电流的定义式去求电荷量.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
8.如图所示的电路中,闭合开关后,将滑动变阻器R的滑片P向上移动,则有( )


| A. | V1表读数变大 | B. | V2表读数变小 | C. | A表读数变小 | D. | 电源的功率变小 |
3. 如图所示,M是一个小型理想变压器,原、副线圈匝数之比n1:n2=10:1,接线柱a、b接电压u=311sin100πt(V)的正弦交变电源.变压器右侧部分为一火警系统原理图,其中R2为用半导体热敏材料制成的传感器(电阻随温度升高而减小),R1为一定值电阻.下列说法正确的是( )
如图所示,M是一个小型理想变压器,原、副线圈匝数之比n1:n2=10:1,接线柱a、b接电压u=311sin100πt(V)的正弦交变电源.变压器右侧部分为一火警系统原理图,其中R2为用半导体热敏材料制成的传感器(电阻随温度升高而减小),R1为一定值电阻.下列说法正确的是( )
 如图所示,M是一个小型理想变压器,原、副线圈匝数之比n1:n2=10:1,接线柱a、b接电压u=311sin100πt(V)的正弦交变电源.变压器右侧部分为一火警系统原理图,其中R2为用半导体热敏材料制成的传感器(电阻随温度升高而减小),R1为一定值电阻.下列说法正确的是( )
如图所示,M是一个小型理想变压器,原、副线圈匝数之比n1:n2=10:1,接线柱a、b接电压u=311sin100πt(V)的正弦交变电源.变压器右侧部分为一火警系统原理图,其中R2为用半导体热敏材料制成的传感器(电阻随温度升高而减小),R1为一定值电阻.下列说法正确的是( )| A. | 当R2所在处出现火警时,电阻R1的功率变小 | |
| B. | 当R2所在处出现火警时,电压表V2的示数变小 | |
| C. | 当R2所在处出现火警时,电流表A的示数变小 | |
| D. | 电压表V1示数为22V |
10.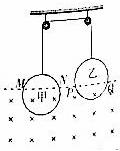 如图所示,两个完全相同的甲、乙金属圆环,用绝缘细线绕过光滑定滑轮相连并悬吊着,处于静止状态,圆环各有一部分处在方向水平的匀强磁场中,圆环与磁场的边界交点分别为M、N、P、Q,且MN=PQ<环的直径,若磁场发生一个微小变化,两环受到的安培力均小于环的重力,则下列说法正确的是( )
如图所示,两个完全相同的甲、乙金属圆环,用绝缘细线绕过光滑定滑轮相连并悬吊着,处于静止状态,圆环各有一部分处在方向水平的匀强磁场中,圆环与磁场的边界交点分别为M、N、P、Q,且MN=PQ<环的直径,若磁场发生一个微小变化,两环受到的安培力均小于环的重力,则下列说法正确的是( )
 如图所示,两个完全相同的甲、乙金属圆环,用绝缘细线绕过光滑定滑轮相连并悬吊着,处于静止状态,圆环各有一部分处在方向水平的匀强磁场中,圆环与磁场的边界交点分别为M、N、P、Q,且MN=PQ<环的直径,若磁场发生一个微小变化,两环受到的安培力均小于环的重力,则下列说法正确的是( )
如图所示,两个完全相同的甲、乙金属圆环,用绝缘细线绕过光滑定滑轮相连并悬吊着,处于静止状态,圆环各有一部分处在方向水平的匀强磁场中,圆环与磁场的边界交点分别为M、N、P、Q,且MN=PQ<环的直径,若磁场发生一个微小变化,两环受到的安培力均小于环的重力,则下列说法正确的是( )| A. | 甲、乙两个环仍保持静止 | |
| B. | 甲环向下运动,乙环向上运动 | |
| C. | 甲环有收缩趋势,乙环有扩张趋势 | |
| D. | 甲环受到的安培力大于乙环受到的安培力 |
8.物体做匀减速直线运动,最初两个2s内的位移分别10m和6m.则下列说法正确的是( )
| A. | 物体的初速度大小为6 m/s | B. | 物体的加速度大小为2m/s2 | ||
| C. | 物体第4s内的位移大小为5m | D. | 物体第4s末的速度大小为1m/s |
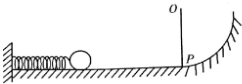 一个实验小组在“探究弹性势能的表达式”的实验中,利用了如图所示实验装置进行实验,光滑水平轨道与光滑圆弧轨道相切,轻弹簧的一端固定在轨道的左端,OP是可绕O点转动的轻杆,且摆到某处就能停在该处,另有一小球,现在利用这些器材测定弹簧被压缩时的弹性势能.
一个实验小组在“探究弹性势能的表达式”的实验中,利用了如图所示实验装置进行实验,光滑水平轨道与光滑圆弧轨道相切,轻弹簧的一端固定在轨道的左端,OP是可绕O点转动的轻杆,且摆到某处就能停在该处,另有一小球,现在利用这些器材测定弹簧被压缩时的弹性势能. 空气中直径小于等于 2.5 微米的细颗粒物称做PM2.5,其在空气中的含量称作PM值,单位是毫克每立方米.某校“PM2.5兴趣小组”自制了一台静电除尘器,装置呈圆筒形,如图为其截面图.高压电极的负极位于中轴线上,由A、B两段金属构成,A段较粗呈杆状,B段较细呈针状,收尘区由半径为R的圆柱形的金属筒壁构成,接高压电源的正极.圆筒中气体分子中的电子和带正电的部分由于受到方向相反的强大的静电力而电离.一部分细颗粒物吸附了电子而带负电,所有带负电的细颗粒物都飞向筒壁,最后在重力的作用下落在筒底,空气因此而变得清洁.在一次试验中,含尘气体由底部吹入,气流速度恒为v,高压电源的恒定不变,工作电流恒为I,经监测,入口处的含尘气体的PM值为k1,出口处的洁净气体的PM值降为k2,若视细颗粒物均为直径为D、密度为ρ的均匀球体,且不计相互之间的影响,忽略含尘气体带入的电荷.
空气中直径小于等于 2.5 微米的细颗粒物称做PM2.5,其在空气中的含量称作PM值,单位是毫克每立方米.某校“PM2.5兴趣小组”自制了一台静电除尘器,装置呈圆筒形,如图为其截面图.高压电极的负极位于中轴线上,由A、B两段金属构成,A段较粗呈杆状,B段较细呈针状,收尘区由半径为R的圆柱形的金属筒壁构成,接高压电源的正极.圆筒中气体分子中的电子和带正电的部分由于受到方向相反的强大的静电力而电离.一部分细颗粒物吸附了电子而带负电,所有带负电的细颗粒物都飞向筒壁,最后在重力的作用下落在筒底,空气因此而变得清洁.在一次试验中,含尘气体由底部吹入,气流速度恒为v,高压电源的恒定不变,工作电流恒为I,经监测,入口处的含尘气体的PM值为k1,出口处的洁净气体的PM值降为k2,若视细颗粒物均为直径为D、密度为ρ的均匀球体,且不计相互之间的影响,忽略含尘气体带入的电荷. 如图所示,一绝缘容器内部为立方体空腔,其长和宽分别为a和b,厚度为d,其两侧等高处装有两根与大气相通的玻璃管(可用来测量液体两侧的压强差).容器内装满密度为ρ的导电液体,容器上下两端装有铂电极A和C,这样就构成了一个液体电阻.该液体电阻置于一方向与容器的厚度方向平行的均匀恒定的磁感应强度为B的磁场中,并通过开关K接在一电动势为ε内阻为r的电池的两端.闭合开关.若稳定时两侧玻璃管中液面的高度差为h,求导电液体的电导率σ.重力加速度大小为g.
如图所示,一绝缘容器内部为立方体空腔,其长和宽分别为a和b,厚度为d,其两侧等高处装有两根与大气相通的玻璃管(可用来测量液体两侧的压强差).容器内装满密度为ρ的导电液体,容器上下两端装有铂电极A和C,这样就构成了一个液体电阻.该液体电阻置于一方向与容器的厚度方向平行的均匀恒定的磁感应强度为B的磁场中,并通过开关K接在一电动势为ε内阻为r的电池的两端.闭合开关.若稳定时两侧玻璃管中液面的高度差为h,求导电液体的电导率σ.重力加速度大小为g.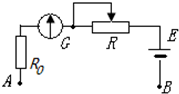 某同学想利用以下器材组装一只欧姆表,并比较精确地测量一只约几千欧电阻的阻值.
某同学想利用以下器材组装一只欧姆表,并比较精确地测量一只约几千欧电阻的阻值.