题目内容
如图所示，已知mA=2mB=3mc，它们距轴的关系是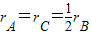
，三物体与转盘表面的动摩擦因数相同，当转盘的速度逐渐增大时（ ）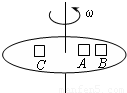
A．物体A先滑动
B．物体B先滑动
C．物体C先滑动
D．B、C同时开始滑动
【答案】分析：物体和圆盘一起做圆周运动，靠静摩擦力提供向心力，求出它们的临界角速度，从而判断谁先滑动．
解答：解：当静摩擦力达到最大静摩擦力时，角速度达到最大值，根据μmg=mrω2解得
，B的半径最大，则B的临界角速度最小，所以物体B先滑动．故B正确，A、C、D错误．
故选B．
点评：解决本题的关键知道物体做圆周运动向心力的来源，运用牛顿第二定律求出物体的临界角速度．
解答：解：当静摩擦力达到最大静摩擦力时，角速度达到最大值，根据μmg=mrω2解得
，B的半径最大，则B的临界角速度最小，所以物体B先滑动．故B正确，A、C、D错误．故选B．
点评：解决本题的关键知道物体做圆周运动向心力的来源，运用牛顿第二定律求出物体的临界角速度．
练习册系列答案
名校课堂系列答案
相关题目
三颗人造地球卫星A、B、C绕地球作匀速圆周运动，如图所示，已知MA=MB＞MC，则对于三个卫星，正确的是（ ）
质量为M=4kg的长木板，上表面粗糙，下表面光滑，静止放在光滑的水平面上．在长木板的左右两端各放一个小物块A、B，如图所示，已知mA=2kg、mB=1kg，两物块与长木板之间的动摩擦因数都是0.2．现同时用力分别击打A、B，使它们在瞬间获得方向相反、大小都是v0=7m/s的水平速度，此后它们在木板上相向滑行，并且在滑行过程中它们始终没有相碰，取g=10m/s2．
质量为M=4kg的长木板，上表面粗糙，下表面光滑，静止地放在光滑的水平地面上．在长木板的左、右两端各放着一个小物块A和B，如图所示．已知mA=2kg、mB=1kg，两物块与长木板之间的动摩擦因数都是0.2．现同时用力分别击打A、B，使它们在瞬间同时获得方向相反、大小都是v0=7m/s的水平速度，此后它们在木板上相向滑行，并且在滑行过程中它们始终没有相碰，取g=10m/s2．问：
如图所示，已知mA=3mB，C为内壁光滑，半径为R的半圆形轨道，D为定滑轮，开始A、B均处于静止状态，释放后，A沿圆弧轨道下滑，若已知A球下滑到最低点时A的速度为v，则此时B的速度为（ ）| A、v | ||||
B、
| ||||
C、
| ||||
| D、2v |
三颗人造卫星A、B、C环绕地球做匀速圆周运动，如图所示，已知mA=mC＜mB，A、B、C的轨道半径分别是RA，RB，RC，它们的周期分别是TA，TB，TC，则三颗卫星（ ）| A、B的线速度始终与C的线速度相同 | ||||||
| B、A的运行周期大于B的运行周期 | ||||||
| C、A的向心力大小大于C的向心力大小 | ||||||
D、半径与周期关系：
|