题目内容
如图所示,在一个圆形区域内,两个方向相反且都垂直于纸面的匀强磁场分布在以直径A2A4为边界的两个半圆形区域Ⅰ、Ⅱ中,A2A4与A1A3的夹角为60°.一质量为m、带电荷量为+q的粒子以某一速度从Ⅰ区的边缘点A1处沿与A1A3成30°角的方向射入磁场,随后该粒子以垂直于A2A4的方向经过圆心O进入Ⅱ区,最后再从A4处射出磁场.已知该粒子从射入到射出磁场所用的时间为t,求Ⅰ区和Ⅱ区中磁感应强度的大小(忽略粒子重力).

答案:
解析:
解析:
|
解:设粒子的入射速度为v,已知粒子带正电,故它在磁场中先顺时针做匀速圆周运动,再逆时针做圆周运动,最后从A4点射出.用B1、B2、R1、R2、T1、T2分别表示在磁场Ⅰ区和Ⅱ区中磁感应强度、轨道半径和周期,有: qvB1=m T1= 设圆形区域的半径为r,如题图所示,已知带电粒子过圆心,且垂直A2A4进入Ⅱ区磁场.连接A1A2,三角形A1OA2为等边三角形,A2为带电粒子在Ⅰ区磁场中运动轨迹的圆心,其轨迹的半径 R1=A1A2=OA2=r 圆心角∠A1A2O=60°,带电粒子在Ⅰ区磁场中运动时间为t1= 带电粒子在Ⅱ区磁场中运动轨迹的圆心在OA4的中点,即R2= 在Ⅱ区磁场中运动的时间为t2= 带电粒子从射入到射出磁场所用的总时间t=t1+t2 由以上各式得: B1= |

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
 (2005?广东)如图所示,在一个圆形区域内,两个方向相反且都垂直于纸面的匀强磁场分布在以直径A2A4为边界的两个半圆形区域Ⅰ、Ⅱ中,A2A4与A1A3的夹角为60°.一质量为m、带电量为+q的粒子以某一速度从Ⅰ区的边缘点A1处沿与A1A3成30°角的方向射入磁场,随后该粒子以垂直于A2A4的方向经过圆心O进入Ⅱ区,最后再从A4处射出磁场.已知该粒子从射入到射出磁场所用的时间为t,求Ⅰ区和Ⅱ区中磁感应强度的大小(忽略粒子重力).
(2005?广东)如图所示,在一个圆形区域内,两个方向相反且都垂直于纸面的匀强磁场分布在以直径A2A4为边界的两个半圆形区域Ⅰ、Ⅱ中,A2A4与A1A3的夹角为60°.一质量为m、带电量为+q的粒子以某一速度从Ⅰ区的边缘点A1处沿与A1A3成30°角的方向射入磁场,随后该粒子以垂直于A2A4的方向经过圆心O进入Ⅱ区,最后再从A4处射出磁场.已知该粒子从射入到射出磁场所用的时间为t,求Ⅰ区和Ⅱ区中磁感应强度的大小(忽略粒子重力).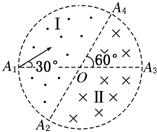 如图所示,在一个圆形区域内,两个方向相反且都垂直于纸面的匀强磁场分布在以直径A2A4为边界的两个半圆形区域Ⅰ、Ⅱ中,直径A2A4与A1A3的夹角为60°.一质量为m、带电荷量为+q的粒子以某一速度从Ⅰ区的边缘点A1处沿与A1A3成30°角的方向射入磁场,随后该粒子以垂直于A2A4的方向经过圆心O进入Ⅱ区,最后从A4处射出磁场.已知该粒子从射入到射出磁场所用的时间为t.(忽略粒子重力).
如图所示,在一个圆形区域内,两个方向相反且都垂直于纸面的匀强磁场分布在以直径A2A4为边界的两个半圆形区域Ⅰ、Ⅱ中,直径A2A4与A1A3的夹角为60°.一质量为m、带电荷量为+q的粒子以某一速度从Ⅰ区的边缘点A1处沿与A1A3成30°角的方向射入磁场,随后该粒子以垂直于A2A4的方向经过圆心O进入Ⅱ区,最后从A4处射出磁场.已知该粒子从射入到射出磁场所用的时间为t.(忽略粒子重力). 学校开展研究性学习,某研究性学习小组的同学根据所学的光学知识,设计了一个测量液体折射率的仪器,如图所示.在一个圆形木盘上过其圆心O作两条相互垂直的直径BC、EF,在半径OA上垂直圆盘面插下两枚大头针P1、P2并保持P1、P2的位置不变,每次测量时,让圆盘的BFC部分竖直进入液体中,而且总使得液面与直径BC相平,EF为界面的法线,而后在图中右上方区域观察P1、P2的像,并在圆周上插上大头针P3,使P3正好挡住P1、P2.同学们通过计算,预先在圆周EC部分刻好了折射率的值.这样只要根据P所插的位置,就可直接读出液体折射率的值.则
学校开展研究性学习,某研究性学习小组的同学根据所学的光学知识,设计了一个测量液体折射率的仪器,如图所示.在一个圆形木盘上过其圆心O作两条相互垂直的直径BC、EF,在半径OA上垂直圆盘面插下两枚大头针P1、P2并保持P1、P2的位置不变,每次测量时,让圆盘的BFC部分竖直进入液体中,而且总使得液面与直径BC相平,EF为界面的法线,而后在图中右上方区域观察P1、P2的像,并在圆周上插上大头针P3,使P3正好挡住P1、P2.同学们通过计算,预先在圆周EC部分刻好了折射率的值.这样只要根据P所插的位置,就可直接读出液体折射率的值.则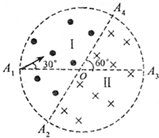 如图所示,在一个圆形区域内,两个方向相反且都垂直于纸面的匀强磁场分布在以直径A2A4为边界的两个半圆形区域Ⅰ、Ⅱ中,A2A4与A1A3的夹角为60°.一质量为m、带电量为+q的粒子以某一速度从Ⅰ区的边缘A1点处沿A1A3成30°角且平行纸面的方向射入磁场,随后该粒子经过圆心O进入Ⅱ区,最后再从A4处射出磁场.则Ⅰ区和Ⅱ区中磁场磁感应强度的大小之比B1:B2为(忽略粒子的重力)( )
如图所示,在一个圆形区域内,两个方向相反且都垂直于纸面的匀强磁场分布在以直径A2A4为边界的两个半圆形区域Ⅰ、Ⅱ中,A2A4与A1A3的夹角为60°.一质量为m、带电量为+q的粒子以某一速度从Ⅰ区的边缘A1点处沿A1A3成30°角且平行纸面的方向射入磁场,随后该粒子经过圆心O进入Ⅱ区,最后再从A4处射出磁场.则Ⅰ区和Ⅱ区中磁场磁感应强度的大小之比B1:B2为(忽略粒子的重力)( )