题目内容
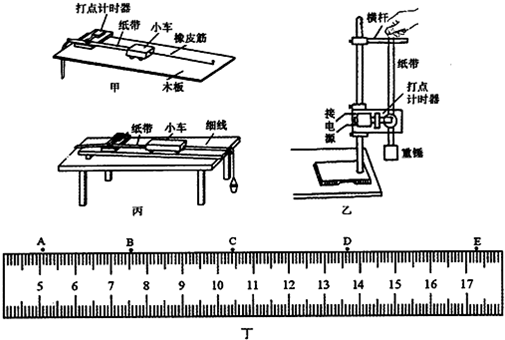
16. 如图所示是利用光电门探究“滑块加速度与外力关系”的实验装置.实验中,将力传感器固定在滑块上,然后把绳的一端固定在传感器的挂钩上,用来测量绳对滑块的拉力,探究在滑块及传感器总质量不变时加速度跟它们所受拉力的关系.本实验,若平衡摩擦力后还需要直接测量的物理量有:滑块上的挡光板的宽度为d,滑块出发点到光电门位置距离为l,使滑块从起点由静止开始运动,光电计时器记录下滑块上挡光板通过光电门的时间为△t.
如图所示是利用光电门探究“滑块加速度与外力关系”的实验装置.实验中,将力传感器固定在滑块上,然后把绳的一端固定在传感器的挂钩上,用来测量绳对滑块的拉力,探究在滑块及传感器总质量不变时加速度跟它们所受拉力的关系.本实验,若平衡摩擦力后还需要直接测量的物理量有:滑块上的挡光板的宽度为d,滑块出发点到光电门位置距离为l,使滑块从起点由静止开始运动,光电计时器记录下滑块上挡光板通过光电门的时间为△t.(1)本实验中是否仍需要细沙和桶的总质量远小于滑块和传感器的总质量否(填“是”或“否”);
(2)滑块的通过光电门时的瞬时速度v=$\frac{d}{△t}$;
(3)滑块的加速度a=$\frac{{d}^{2}}{2l(△t)^{2}}$;
(4)换用不同钩码拉,测出多组不同外拉力F对应的△t,用图象法处理获得的数据,若以拉力F为纵坐标,则应以$\frac{1}{△{t}^{2}}$为横坐标,才能得出加速度与合力的正比关系.
分析 该实验中由于已经用传感器测出绳子拉力大小,故不需要满足砝码和砝码盘的总质量远小于小车的质量;
利用小球通过光电门的平均速度来代替瞬时速度,由此可以求出滑块通过光电门时的瞬时速度;
根据运动学公式v2=2al,从而即可求得重力加速度的大小;
由牛顿第二定律,结合加速度表达式,及数学知识,即可求解.
解答 解:(1)该实验中由于已经用传感器测出绳子拉力大小,不是将砝码和砝码盘的重力作为小车的拉力,故不需要满足砝码和砝码盘的总质量远小于小车的质量.
(2)极短时间内的平均速度表示瞬时速度,
则滑块经过光电门时的速度表达式为:v=$\frac{d}{△t}$,
(3)根据运动学公式得:a=$\frac{{v}^{2}}{2l}$=$\frac{{d}^{2}}{2l(△t)^{2}}$
(4)由牛顿第二定律,则有:F=m$\frac{{d}^{2}}{2l(△t)^{2}}$;
若以拉力F为纵坐标,则应以$\frac{1}{△{t}^{2}}$为横坐标时,才能得出加速度与合力的正比关系;
故答案为:(1)否;(2)$\frac{d}{△t}$;(3)$\frac{{d}^{2}}{2l(△t)^{2}}$;(4)$\frac{1}{△{t}^{2}}$.
点评 考查通过平均速度求瞬时速度的方法,掌握运动学公式求加速度的应用,理解牛顿第二定律与运动学公式的应用,注意图象的成正比与线性关系的不同.最后理解是否需要细沙和桶的总质量远小于滑块和传感器的总质量的原因.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
6. 将三个小球a、b、c用轻弹簧和细绳相连悬挂于O点,a球的质量为m,b、c球的质量均为$\frac{m}{2}$,用力F拉小球口,使弹簧Oa与竖直方向夹角为θ=30°,如图所示,整个装置处于平衡状态,则此时F的大小可能为( )
将三个小球a、b、c用轻弹簧和细绳相连悬挂于O点,a球的质量为m,b、c球的质量均为$\frac{m}{2}$,用力F拉小球口,使弹簧Oa与竖直方向夹角为θ=30°,如图所示,整个装置处于平衡状态,则此时F的大小可能为( )
 将三个小球a、b、c用轻弹簧和细绳相连悬挂于O点,a球的质量为m,b、c球的质量均为$\frac{m}{2}$,用力F拉小球口,使弹簧Oa与竖直方向夹角为θ=30°,如图所示,整个装置处于平衡状态,则此时F的大小可能为( )
将三个小球a、b、c用轻弹簧和细绳相连悬挂于O点,a球的质量为m,b、c球的质量均为$\frac{m}{2}$,用力F拉小球口,使弹簧Oa与竖直方向夹角为θ=30°,如图所示,整个装置处于平衡状态,则此时F的大小可能为( )| A. | $\frac{\sqrt{3}}{3}$mg | B. | $\frac{\sqrt{3}}{2}$mg | C. | mg | D. | $\frac{\sqrt{3}}{4}$mg |
4. 利用静电除尘可以大量减少排放烟气中的粉尘.如图是静电除尘装置的示意图,烟气从管口M进入,从管口N排出,当A、B两端接上高压后,在电场作用下管道内的空气分子被电离为电子和正离子,而粉尘在吸附了电子后最终附着在金属管壁上,从而达到减少排放烟气中粉尘的目的.根据上述原理,下面做法正确的是( )
利用静电除尘可以大量减少排放烟气中的粉尘.如图是静电除尘装置的示意图,烟气从管口M进入,从管口N排出,当A、B两端接上高压后,在电场作用下管道内的空气分子被电离为电子和正离子,而粉尘在吸附了电子后最终附着在金属管壁上,从而达到减少排放烟气中粉尘的目的.根据上述原理,下面做法正确的是( )
 利用静电除尘可以大量减少排放烟气中的粉尘.如图是静电除尘装置的示意图,烟气从管口M进入,从管口N排出,当A、B两端接上高压后,在电场作用下管道内的空气分子被电离为电子和正离子,而粉尘在吸附了电子后最终附着在金属管壁上,从而达到减少排放烟气中粉尘的目的.根据上述原理,下面做法正确的是( )
利用静电除尘可以大量减少排放烟气中的粉尘.如图是静电除尘装置的示意图,烟气从管口M进入,从管口N排出,当A、B两端接上高压后,在电场作用下管道内的空气分子被电离为电子和正离子,而粉尘在吸附了电子后最终附着在金属管壁上,从而达到减少排放烟气中粉尘的目的.根据上述原理,下面做法正确的是( )| A. | A端接高压负极,B端接高压正极 | B. | A端接高压正极,B端接高压负极 | ||
| C. | A端、B端都接高压正极 | D. | A端、B端都接高压负极 |
11.已知金星和水星绕太阳公转的轨道如图所示,公转周期分布是224天和88天,则下列说法不正确的是( )


| A. | 水星的公转线速度大于金星公转线速度 | |
| B. | 水星和金星的公转线速度都小于地球的公转线速度 | |
| C. | 从水星处于太阳和金星连线上中间某一点开始计时,至少再经过约145天才能再次出现在太阳和金星连线上中间某一点的位置 | |
| D. | 地球在金星外侧 |
6.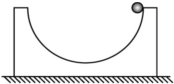 如图所示,内壁光滑的半圆形凹槽放置于粗糙的水平地面上,现将一个小铁球从与圆心等高处由静止释放,在铁球沿凹槽内壁下滑的过程中凹槽保持静止,则在铁球由最高点下滑到最低点的过程中,下列说法中正确的是( )
如图所示,内壁光滑的半圆形凹槽放置于粗糙的水平地面上,现将一个小铁球从与圆心等高处由静止释放,在铁球沿凹槽内壁下滑的过程中凹槽保持静止,则在铁球由最高点下滑到最低点的过程中,下列说法中正确的是( )
 如图所示,内壁光滑的半圆形凹槽放置于粗糙的水平地面上,现将一个小铁球从与圆心等高处由静止释放,在铁球沿凹槽内壁下滑的过程中凹槽保持静止,则在铁球由最高点下滑到最低点的过程中,下列说法中正确的是( )
如图所示,内壁光滑的半圆形凹槽放置于粗糙的水平地面上,现将一个小铁球从与圆心等高处由静止释放,在铁球沿凹槽内壁下滑的过程中凹槽保持静止,则在铁球由最高点下滑到最低点的过程中,下列说法中正确的是( )| A. | 小球竖直方向的加速度逐渐增加 | |
| B. | 小球竖直方向的加速度逐渐减小 | |
| C. | 小球水平方向的加速度先增加后减小 | |
| D. | 小球水平方向的加速度先减小后增加 |

 实验电路如图所示,随着滑动变阻器滑片的移动,电压表的示数U,电流表示数I及干电池的输出功率P都会发生变化,下面各示意图中正确的是( )
实验电路如图所示,随着滑动变阻器滑片的移动,电压表的示数U,电流表示数I及干电池的输出功率P都会发生变化,下面各示意图中正确的是( )



 如图为简谐横波在t=0时刻的波形图,传播方向如图所示,t=3s时,Q点的振动形式第一次传播到P点,该波的传播速度为1m/s;Q点的振动方程为y=2sin$\frac{π}{2}$tcm.
如图为简谐横波在t=0时刻的波形图,传播方向如图所示,t=3s时,Q点的振动形式第一次传播到P点,该波的传播速度为1m/s;Q点的振动方程为y=2sin$\frac{π}{2}$tcm.