题目内容
如图，绝缘水平地面上有宽L=0.4m的匀强电场区域，场强E=6×105N/C、方向水平向左．不带电的物块B静止在电场边缘的O点，带电量q=5×10-8C、质量mA=1×10-2kg的物块A在距O点s=2.25m处以v0=5m/s的水平初速度向右运动，与B发生碰撞，假设碰撞前后A、B构成的系统没有动能损失．A的质量是B的k（k＞1）倍，A、B与水平面间的动摩擦因数都为μ=0.2，物块均可视为质点，且A的电荷量始终不变，取g=10m/s2．（1）求A到达O点与B碰撞前的速度；
（2）求碰撞后瞬间，A和B的速度；
（3）讨论k在不同取值范围时电场力对A做的功．
【答案】分析：（1）根据动能定理求出A到达O点与B碰撞前的速度．
（2）碰撞的瞬间，动量守恒定律，因为系统没有动能损失，则机械能守恒，综合动量守恒定律和机械能守恒定律求出碰撞后瞬间A、B的速度．
（3）讨论A能从电场右边界离开和不能从电场右边界离开，根据动能定理得出k的范围，从而根据电场力做功的特点求出电场力所做的功．
解答：解：（1）设碰撞前A的速度为v，由动能定理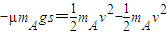
…①
得：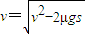
=4m/s …②
（2）设碰撞后A、B速度分别为vA、vB，且设向右为正方向；由于弹性碰撞，所以有：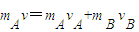
…③
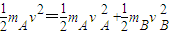…④
联立③④并将mA=kmB及v=4m/s
代入得：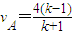
m/s…⑤
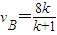m/s…⑥
（3）讨论：
（i）如果A能从电场右边界离开，必须满足：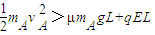
…⑦
联立⑤⑦代入数据，得：k＞3…⑧
电场力对A做功为：WE=-qEL=6×105×5×10-8×0.4（J）=-1.2×10-2（J） …⑨
（ii）如果A不能从电场右边界离开电场，必须满足：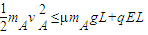
…⑩
联立⑤⑩代入数据，得：k≤3…（11）
考虑到k＞1，所以在1＜k≤3范围内A不能从电场右边界离开…（12）
又：qE=3×10-2N＞μmg=2×10-2N…（13）
所以A会返回并从电场的左侧离开，整个过程电场力做功为0．即：WE=0…（14）
答：（1）A到达O点与B碰撞前的速度为4m/s．
（2）碰撞后瞬间，A和B的速度分别为：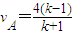
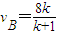m/s，
m/s．
（3）k＞3，电场力做功为）=-1.2×10-2．
1＜k≤3，电场力做功为零．
点评：本题综合考查了动量守恒定律、动能定理、机械能守恒定律，综合性较强，对学生的能力要求较高，尤其第三问，要考虑电场能从右边界离开和不能从右边界离开．
（2）碰撞的瞬间，动量守恒定律，因为系统没有动能损失，则机械能守恒，综合动量守恒定律和机械能守恒定律求出碰撞后瞬间A、B的速度．
（3）讨论A能从电场右边界离开和不能从电场右边界离开，根据动能定理得出k的范围，从而根据电场力做功的特点求出电场力所做的功．
解答：解：（1）设碰撞前A的速度为v，由动能定理
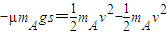…①得：
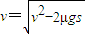=4m/s …②（2）设碰撞后A、B速度分别为vA、vB，且设向右为正方向；由于弹性碰撞，所以有：
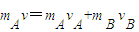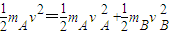…③…④联立③④并将mA=kmB及v=4m/s
代入得：
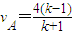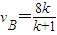m/s…⑤m/s…⑥（3）讨论：
（i）如果A能从电场右边界离开，必须满足：
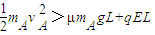…⑦联立⑤⑦代入数据，得：k＞3…⑧
电场力对A做功为：WE=-qEL=6×105×5×10-8×0.4（J）=-1.2×10-2（J） …⑨
（ii）如果A不能从电场右边界离开电场，必须满足：
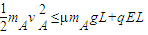…⑩联立⑤⑩代入数据，得：k≤3…（11）
考虑到k＞1，所以在1＜k≤3范围内A不能从电场右边界离开…（12）
又：qE=3×10-2N＞μmg=2×10-2N…（13）
所以A会返回并从电场的左侧离开，整个过程电场力做功为0．即：WE=0…（14）
答：（1）A到达O点与B碰撞前的速度为4m/s．
（2）碰撞后瞬间，A和B的速度分别为：
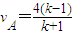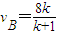m/s，m/s．（3）k＞3，电场力做功为）=-1.2×10-2．
1＜k≤3，电场力做功为零．
点评：本题综合考查了动量守恒定律、动能定理、机械能守恒定律，综合性较强，对学生的能力要求较高，尤其第三问，要考虑电场能从右边界离开和不能从右边界离开．
练习册系列答案
相关题目
（2011?广州一模）如图，绝缘水平地面上有宽L=0.4m的匀强电场区域，场强E=6×105N/C、方向水平向左．不带电的物块B静止在电场边缘的O点，带电量q=5×10-8C、质量mA=1×10-2kg的物块A在距O点s=2.25m处以v0=5m/s的水平初速度向右运动，与B发生碰撞，假设碰撞前后A、B构成的系统没有动能损失．A的质量是B的k（k＞1）倍，A、B与水平面间的动摩擦因数都为μ=0.2，物块均可视为质点，且A的电荷量始终不变，取g=10m/s2．
、质量
的物块A，在距O点s = 2．25m处以vo =5m/s的水平初速度向右运动，并与B发生碰撞，假设碰撞前后A、B构成的系统没有动能损失，A的质量是B的K（K>1）倍，A、B与地面间的动摩擦因数都为μ=0.2，物块均可视为质点，且A的电荷量始终不变，取g = 10m/S2。
、质量
的物块A，在距O点s = 2．25m处以vo =5m/s的水平初速度向右运动，并与B发生碰撞，假设碰撞前后A、B构成的系统没有动能损失，A的质量是B的K（K>1）倍，A、B与地面间的动摩擦因数都为μ=0.2，物块均可视为质点，且A的电荷量始终不变，取g = 10m/S2。
