题目内容
18. 水平光滑直轨道ab与半径为R的竖直半圆形光滑轨道bc相切,一小球以初速度v0沿直轨道向右运动,如图所示,小球进入圆形轨道后刚好能通过C点,然后小球做平抛运动落在直轨道上的d点,则( )
水平光滑直轨道ab与半径为R的竖直半圆形光滑轨道bc相切,一小球以初速度v0沿直轨道向右运动,如图所示,小球进入圆形轨道后刚好能通过C点,然后小球做平抛运动落在直轨道上的d点,则( )| A. | 小球到达c点的速度为$\sqrt{gR}$ | |
| B. | 小球在c点将向下做自由落体运动 | |
| C. | 小球在直轨道上的落点d与b点距离为2R | |
| D. | 小球从c点落到d点需要时间$\sqrt{\frac{R}{g}}$ |
分析 小球恰好通过C点,根据重力恰好等于向心力求出C点的速度,小球离开C点后做平抛运动,根据分位移公式列式求解分析.
解答 解;A、小球恰好通过最高点C,根据重力提供向心力,有:
mg=m$\frac{{v}^{2}}{R}$
解得:v=$\sqrt{gR}$,故A正确;
B、小球离开C点后做平抛运动,有:
x=vt
2R=$\frac{1}{2}$gt2
解得:
t=$2\sqrt{\frac{R}{g}}$
x=2R
故BD错误,C正确;
故选:AC.
点评 本题关键是明确小球的运动情况,然后运用平抛运动的分位移公式和向心力公式列式求解,难度不大,属于基础题.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
13.下列关于物理学史和物理研究方法的叙述中不正确的是( )
| A. | 用点电荷来代替带电体的研究方法叫理想模型法 | |
| B. | 利用v-t图象推导匀变速直线运动位移公式的方法是微元法 | |
| C. | 伽利略借助实验研究和逻辑推理得出了自由落体运动规律 | |
| D. | 法拉第发现电流的磁效应与他坚信电和磁之间一定存在联系的哲学思想是分不开的 |
9.某学习小组为探究影响干涉条纹宽度的因素,在实验室用蓝光做了双缝千涉实验,在光屏上呈现出蓝、暗相间的平行条纹,设相邻两条蓝条纹间的距离为△x.你认为以下结论中正确的是( )
| A. | 单缝到双缝间的距离越大,△x就越大 | |
| B. | 双缝之间的距离越大,△x就越大 | |
| C. | 双缝到光屏之间的距离越大,△x就越大 | |
| D. | 双缝之间的距离越小,△x就越大 |
6.下列说法正确的是( )
| A. | 力对物体不做功,说明物体没有位移 | |
| B. | 力对物体做功越多,说明物体所受的力越大 | |
| C. | 水平恒力F先后使甲(在粗糙水平面),乙(在光滑水平面)两物体,都向前移动相同的位移,制造力F对甲、乙做功相等 | |
| D. | 把重1N的物体匀速举高1m,重力做功为1J |
13. 用a、b两束单色光分别照射同一双缝干涉实验装置,在距双缝恒定距离的屏上得到如图所示的干涉图样,其中图甲是用a光照射时形成的,图乙是用b光照射时形成的,关于a、b两束单色光,下列说法正确的是( )
用a、b两束单色光分别照射同一双缝干涉实验装置,在距双缝恒定距离的屏上得到如图所示的干涉图样,其中图甲是用a光照射时形成的,图乙是用b光照射时形成的,关于a、b两束单色光,下列说法正确的是( )
 用a、b两束单色光分别照射同一双缝干涉实验装置,在距双缝恒定距离的屏上得到如图所示的干涉图样,其中图甲是用a光照射时形成的,图乙是用b光照射时形成的,关于a、b两束单色光,下列说法正确的是( )
用a、b两束单色光分别照射同一双缝干涉实验装置,在距双缝恒定距离的屏上得到如图所示的干涉图样,其中图甲是用a光照射时形成的,图乙是用b光照射时形成的,关于a、b两束单色光,下列说法正确的是( )| A. | 在同一介质中,a、b两光的传播速度相同 | |
| B. | a光的频率比b光的大 | |
| C. | 在水中,a光的传播速度比b光的小 | |
| D. | 水对a光的折射率比对b光的大 | |
| E. | b光的波长比a光的短 |
3.质量为m的卫星,绕质量为M的地球做匀速圆周运动,轨道半径为r,则卫星的向心加速度大小为(引力常量为G)( )
| A. | $\frac{M}{G{r}^{2}}$ | B. | $\frac{m}{G{r}^{2}}$ | C. | $\frac{GM}{{r}^{2}}$ | D. | $\frac{Gm}{{r}^{2}}$ |
8.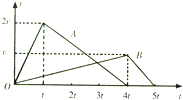 质量相等的A、B两物体(均可视为质点)放在同一水平面上,分别受到水平恒力F1、F2的作用,同时由静止开始从同一位置出发沿相同方向做匀加速直线运动.经过时间t0和4t0速度分别达到2v0和v0时分别撤去F1和F2,以后物体继续做匀减速运动直至停止.两物体速度随时间变化的图象如图所示,对于上述过程下列说法中正确的是( )
质量相等的A、B两物体(均可视为质点)放在同一水平面上,分别受到水平恒力F1、F2的作用,同时由静止开始从同一位置出发沿相同方向做匀加速直线运动.经过时间t0和4t0速度分别达到2v0和v0时分别撤去F1和F2,以后物体继续做匀减速运动直至停止.两物体速度随时间变化的图象如图所示,对于上述过程下列说法中正确的是( )
 质量相等的A、B两物体(均可视为质点)放在同一水平面上,分别受到水平恒力F1、F2的作用,同时由静止开始从同一位置出发沿相同方向做匀加速直线运动.经过时间t0和4t0速度分别达到2v0和v0时分别撤去F1和F2,以后物体继续做匀减速运动直至停止.两物体速度随时间变化的图象如图所示,对于上述过程下列说法中正确的是( )
质量相等的A、B两物体(均可视为质点)放在同一水平面上,分别受到水平恒力F1、F2的作用,同时由静止开始从同一位置出发沿相同方向做匀加速直线运动.经过时间t0和4t0速度分别达到2v0和v0时分别撤去F1和F2,以后物体继续做匀减速运动直至停止.两物体速度随时间变化的图象如图所示,对于上述过程下列说法中正确的是( )| A. | 物体A、B的位移大小之比是6:5 | |
| B. | 两物体运动的全过程,合外力对A物体做的功多 | |
| C. | 在2t0和3t0间的某一时刻B追上A | |
| D. | 两物体运动过程中,A一直在B的前面 |
 质量为m的小球能在半径为R的粗糙环状细管内滑动,细管被竖直放置.设在如图所示位置给小球沿切线方向竖直向上的初速度v0,小球恰能在细管内滑动一周而停止,则小球受到的摩擦力所做的功-mgh-$\frac{1}{2}$mv02.
质量为m的小球能在半径为R的粗糙环状细管内滑动,细管被竖直放置.设在如图所示位置给小球沿切线方向竖直向上的初速度v0,小球恰能在细管内滑动一周而停止,则小球受到的摩擦力所做的功-mgh-$\frac{1}{2}$mv02.