题目内容
如图所示,两个物体以相同大小的初始速度从O点同时分别向x轴正负方向水平抛出,它们的轨迹恰好是抛物线方程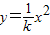 ,(曲率半径简单地理解,在曲线上一点附近与之重合的圆弧的最大半径)那么以下说法正确的是( )
,(曲率半径简单地理解,在曲线上一点附近与之重合的圆弧的最大半径)那么以下说法正确的是( )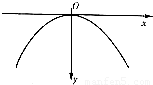
A.初始速度为
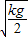
B.初始速度为
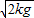
C.O点的曲率半径为
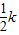
D.O点的曲率半径为2k
【答案】分析:两球均做平抛运动,水平方向的分运动是匀速直线运动,竖直方向上的分运动是自由落体运动,得到水平位移大小x和竖直位移大小y与时间的关系,代入抛物线方程,即可求得初速度;根据数学知识求解O点的曲率半径.
解答:解:A、B设小球运动的时间为t,则有
x=vt,y=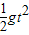
代入到抛物线方程y=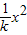 ,解得,初速度v=
,解得,初速度v=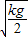 .故A正确,B错误.
.故A正确,B错误.
CD、抛物线方程y=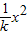 求导得:y′=
求导得:y′=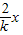 .根据数学知识得知,O点的曲率半径为R=
.根据数学知识得知,O点的曲率半径为R=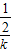 =
=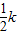 .故C正确,D错误.
.故C正确,D错误.
故选AC.
点评:本题运用数学上参数方程的方法求解初速度,关键是抓住平抛运动的分解方法.根据曲率半径的定义,由数学知识求解.
解答:解:A、B设小球运动的时间为t,则有
x=vt,y=
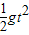
代入到抛物线方程y=
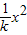 ,解得,初速度v=
,解得,初速度v=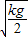 .故A正确,B错误.
.故A正确,B错误.CD、抛物线方程y=
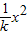 求导得:y′=
求导得:y′=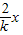 .根据数学知识得知,O点的曲率半径为R=
.根据数学知识得知,O点的曲率半径为R=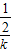 =
=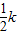 .故C正确,D错误.
.故C正确,D错误.故选AC.
点评:本题运用数学上参数方程的方法求解初速度,关键是抓住平抛运动的分解方法.根据曲率半径的定义,由数学知识求解.

练习册系列答案
相关题目
 如图所示,两个物体以相同大小的初始速度从O点同时分别向x轴正负方向水平抛出,它们的轨迹恰好是抛物线方程
如图所示,两个物体以相同大小的初始速度从O点同时分别向x轴正负方向水平抛出,它们的轨迹恰好是抛物线方程 如图所示,两个物体以相同大小的初始速度从O点同时分别向x轴正负方向水平抛出,它们的轨迹恰好是抛物线方程
如图所示,两个物体以相同大小的初始速度从O点同时分别向x轴正负方向水平抛出,它们的轨迹恰好是抛物线方程
 ,(曲率半径简单地理解,在曲线上一点附近与之重合的圆弧的最大半径)那么以下说法正确的是 ( )
,(曲率半径简单地理解,在曲线上一点附近与之重合的圆弧的最大半径)那么以下说法正确的是 ( )



 ,(曲率半径简单地理解,在曲线上一点附近与之重合的圆弧的最大半径)那么以下说法正确的是(
)
,(曲率半径简单地理解,在曲线上一点附近与之重合的圆弧的最大半径)那么以下说法正确的是(
)



