题目内容
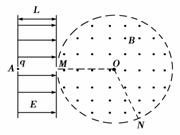
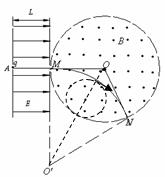
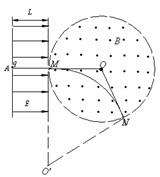
如图所示，空间分布着方向平行于纸面且与场区边界垂直的有界匀强电场，电场强度为E、宽度为L。在紧靠电场右侧的圆形区域内，分布着垂直于纸面向外的匀强磁场，圆形磁场区域半径为r。当一带正电的粒子（质量为m，电荷量为q）从A点静止释放后，在M点离开电场，并沿半径方向射入磁场区域，磁感应强度为B，粒子恰好从N点射出，O为圆心，∠MON＝120°，粒子重力忽略不计。求：
（1）粒子经电场加速后，进入磁场时速度v的大小；
（2）匀强磁场的磁感应强度B的大小和粒子在电场、磁场中运动的总时间t；
（3）若粒子在离开磁场前某时刻，磁感应强度方向不变，大小突然变为B1，此后粒子恰好被束缚在该磁场中，则B1的最小值为多少？
解：
（1）设粒子经电场加速后的速度为v，根据动能定理有qEL=
mv2 （2分）
解得：
（2分）
（2）粒子在磁场中完成了如图所示的部分圆运动，设其半径为 R，因洛伦兹力提供向心力，
所以有qvB= 
（1分）
由几何关系得
（2分）
所以
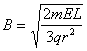（1分）
设粒子在电场中加速的时间为
，在磁场中偏转的时间为
粒子在电场中运动的时间t1=
=
（2分）
粒子在磁场中做匀速圆周运动，其周期为
（1分）
由于∠MON＝120°，所以∠MO＇N＝60°故粒子在磁场中运动时间
t2=
(2分)
所以粒子从A点出发到N点离开磁场经历的时间：
t=t1+t2 =+
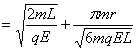（1分）
（3）如图所示，当粒子运动到轨迹与O O＇连线交点处改变磁场大小时，粒子运动的半径最大，既B1对应最小值（2分）
由几何关系得此时最大半径有 
（2分）
所以 
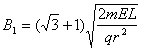（2分）
（2012?台州二模）如图所示，空间分布着宽为L，垂直于纸面向里的匀强磁场．一金属线框从磁场左边界匀速向右通过磁场区域．规定逆时针方向为电流的正方向，则感应电流随位移变化的关系图（i-x）正确的是（ ）
（2011?东莞一模）如图所示，空间分布着方向平行于纸面且与场区边界垂直的有界匀强电场，电场强度为E、场区宽度为L．在紧靠电场右侧的圆形区域内，分布着垂直于纸面向外的匀强磁场，磁感应强度B未知，圆形磁场区域半径为r．一质量为m、电荷量为q的带正电的粒子从A点由静止释放后，在M点离开电场，并沿半径方向射入磁场区域，然后从N点射出，O为圆心，∠MON=120°，粒子重力可忽略不计．求：
25②（供选用《选修3-l》物理课教材的学生做）
如图所示，空间分布着有理想边界的匀强电场和匀强磁场，已知左侧匀强电场的场强大小为E、方向水平向右，其宽度为L；中间区域匀强磁场的磁感应强度大小为B、方向垂直纸面向外；右侧匀强磁场的磁感应强度大小也为B、方向垂直纸面向里．一个带正电的粒子（质量为m、电荷量为q，不计重力）从电场左边缘a点由静止开始运动，穿过中间磁场区域进入右侧磁场区域后，又回到了a点，然后重复上述运动过程．求：