题目内容
13.质量是1×103kg的汽车驶过一座拱桥,已知桥顶点桥面的圆弧半径是90m,求:(1)汽牢以I5m/s的速度驶过桥顶时,汽车对桥面的压力;
(2)汽车以多大的速度驶过桥顶时,汽车对桥面的压力为零?
分析 (1)汽车在桥顶,靠重力和支持力的合力提供向心力,结合牛顿第二定律求出支持力的大小,从而得出压力的大小.
(2)当汽车对桥面的压力为零,靠重力提供向心力,结合牛顿第二定律求出汽车的速度.
解答 解:(1)在桥顶,根据牛顿第二定律得:
$mg-N=m\frac{{v}^{2}}{R}$,
解得支持力为:
N=$mg-m\frac{{v}^{2}}{R}=1×1{0}^{4}-1{0}^{3}×\frac{1{5}^{2}}{90}$N=7.5×103N,
根据牛顿第三定律知,汽车对桥面的压力为7.5×103N.
(2)当压力为零时,根据mg=$m\frac{{v}^{2}}{R}$得:v=$\sqrt{gR}=\sqrt{10×90}$m/s=30m/s.
答:(1)汽牢以I5m/s的速度驶过桥顶时,汽车对桥面的压力为7.5×103N;
(2)汽车以30m/s的速度驶过桥顶时,汽车对桥面的压力为零.
点评 解决本题的关键知道汽车在最高点向心力的来源,结合牛顿第二定律进行求解,难度不大.

练习册系列答案
相关题目
1. 在如图所示的有界磁场区域,磁场方向水平,上、下部分磁感应强度大小均为B,宽度均为L.现有一竖直平面内的匝数为n,质量为m,边长为L的正方形金属线框,从磁场上方某处由静止释放,当ab边刚进入磁场e1e2时,线框恰好做匀速运动:经过一段时间后,当ab边到达下方磁场中距边界O1O2距离为s的f1f2位置时,线框再次做匀速运动.已知线框总电阻为R,不计空气阻力,若ab边到达位置e1e2时速度大小为v1,到达位置f1f2时,线框的速度为v2,则( )
在如图所示的有界磁场区域,磁场方向水平,上、下部分磁感应强度大小均为B,宽度均为L.现有一竖直平面内的匝数为n,质量为m,边长为L的正方形金属线框,从磁场上方某处由静止释放,当ab边刚进入磁场e1e2时,线框恰好做匀速运动:经过一段时间后,当ab边到达下方磁场中距边界O1O2距离为s的f1f2位置时,线框再次做匀速运动.已知线框总电阻为R,不计空气阻力,若ab边到达位置e1e2时速度大小为v1,到达位置f1f2时,线框的速度为v2,则( )
 在如图所示的有界磁场区域,磁场方向水平,上、下部分磁感应强度大小均为B,宽度均为L.现有一竖直平面内的匝数为n,质量为m,边长为L的正方形金属线框,从磁场上方某处由静止释放,当ab边刚进入磁场e1e2时,线框恰好做匀速运动:经过一段时间后,当ab边到达下方磁场中距边界O1O2距离为s的f1f2位置时,线框再次做匀速运动.已知线框总电阻为R,不计空气阻力,若ab边到达位置e1e2时速度大小为v1,到达位置f1f2时,线框的速度为v2,则( )
在如图所示的有界磁场区域,磁场方向水平,上、下部分磁感应强度大小均为B,宽度均为L.现有一竖直平面内的匝数为n,质量为m,边长为L的正方形金属线框,从磁场上方某处由静止释放,当ab边刚进入磁场e1e2时,线框恰好做匀速运动:经过一段时间后,当ab边到达下方磁场中距边界O1O2距离为s的f1f2位置时,线框再次做匀速运动.已知线框总电阻为R,不计空气阻力,若ab边到达位置e1e2时速度大小为v1,到达位置f1f2时,线框的速度为v2,则( )| A. | v1<v2,v2=$\frac{mgR}{{2n{B^2}{L^2}}}$ | B. | v1>v2,v2=$\frac{mgR}{{2n{B^2}{L^2}}}$ | ||
| C. | v1<v2,v2=$\frac{mgR}{{4n{B^2}{L^2}}}$ | D. | v1>v2,v2=$\frac{mgR}{{4{n^2}{B^2}{L^2}}}$ |
8.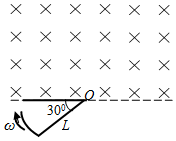 如图所示的区域内有垂直于纸面的匀强磁场,磁感应强度为B.电阻为R、半径为L、圆心角为30°的扇形闭合导线框绕垂直于纸面的o轴以角速度ω匀速转动(o轴位于磁场边界).则线框内产生的感应电流的有效值为( )
如图所示的区域内有垂直于纸面的匀强磁场,磁感应强度为B.电阻为R、半径为L、圆心角为30°的扇形闭合导线框绕垂直于纸面的o轴以角速度ω匀速转动(o轴位于磁场边界).则线框内产生的感应电流的有效值为( )
 如图所示的区域内有垂直于纸面的匀强磁场,磁感应强度为B.电阻为R、半径为L、圆心角为30°的扇形闭合导线框绕垂直于纸面的o轴以角速度ω匀速转动(o轴位于磁场边界).则线框内产生的感应电流的有效值为( )
如图所示的区域内有垂直于纸面的匀强磁场,磁感应强度为B.电阻为R、半径为L、圆心角为30°的扇形闭合导线框绕垂直于纸面的o轴以角速度ω匀速转动(o轴位于磁场边界).则线框内产生的感应电流的有效值为( )| A. | $\frac{B{L}^{2}ω}{72R}$ | B. | $\frac{\sqrt{6}B{L}^{2}ω}{12R}$ | C. | $\frac{\sqrt{2}B{L}^{2}ω}{4R}$ | D. | $\frac{\sqrt{3}B{L}^{2}ω}{2R}$ |
18. 如图所示,将一平行板电容器与电源连接,开关S闭合,电容器两板间一带电微粒静止不动,下列各叙述中正确的是( )
如图所示,将一平行板电容器与电源连接,开关S闭合,电容器两板间一带电微粒静止不动,下列各叙述中正确的是( )
 如图所示,将一平行板电容器与电源连接,开关S闭合,电容器两板间一带电微粒静止不动,下列各叙述中正确的是( )
如图所示,将一平行板电容器与电源连接,开关S闭合,电容器两板间一带电微粒静止不动,下列各叙述中正确的是( )| A. | 保持开关闭合,将上极板向上移,则微粒将向下运动 | |
| B. | 保持开关闭合,将上极板向上移,则电流表将会有从b到a的电流通过 | |
| C. | 断开开关S,微粒将向下运动 | |
| D. | 断开开关S,将上极板向上移,则微粒将向下运动 |
5.若宇航员在某行星和地球上相对于各自的水平地面附近相同的高度,将一个物体由静止释放,它们落地时间之比为2:1,已知该行星质量是地球质量的9倍,地球表面重力加速度为g,地球半径为R,下列分析正确的是( )
| A. | 该行星表面的重力加速度为$\frac{1}{2}$g | B. | 该行星表面的重力加速度为$\frac{1}{4}$g | ||
| C. | 该行星的半径为6R | D. | 该行星的密度比地球的密度大 |
2.某人用绳提着质量为m的物体,使物体以加速度a(a<g)沿竖直方向加速下降高度h;稍停后,此人再用绳提着该物体以加速度a沿竖直方向加速提升高度h.这两个过程中人对物体做的总功为( )
| A. | 2mah | B. | 0 | C. | 2mgh | D. | m(g+a)h |
3.关于理想气体的内能,下列说法正确的是( )
| A. | 气体在膨胀时,内能可能不变 | |
| B. | 质量和温度都相同的气体,内能一定相同 | |
| C. | 一定质量的某种理想气体在等压压缩过程中,内能一定减少 | |
| D. | 气体温度不变,整体运动速度越大,其内能越大 |
 磁场的方向可以用小磁针静止时N极的指向来描述,如图所示,通电螺线管内部和外部放置a、b、c、d四个小磁针,其中小磁针指向错误的是( )
磁场的方向可以用小磁针静止时N极的指向来描述,如图所示,通电螺线管内部和外部放置a、b、c、d四个小磁针,其中小磁针指向错误的是( ) 小平板车静止在光滑的水平面上,其质量为3kg,一质量为1kg的小物块以水平初速度v0=4m/s沿小车表面向右滑去,如图所示.由于小物块与平板车表面间存在着摩擦,使小物块最终相对于平板车静止.求:
小平板车静止在光滑的水平面上,其质量为3kg,一质量为1kg的小物块以水平初速度v0=4m/s沿小车表面向右滑去,如图所示.由于小物块与平板车表面间存在着摩擦,使小物块最终相对于平板车静止.求: