题目内容
 如图,在平面坐标系xoy内,第Ⅱ、Ⅲ象限内存在沿Y轴正方向的匀强电场,第1、Ⅳ象限内存在半径为L的圆形匀强磁场,磁场圆心在M(L,0)点,磁场方向垂直于坐标平面向外.一带正电粒子从第lll象限中的
如图,在平面坐标系xoy内,第Ⅱ、Ⅲ象限内存在沿Y轴正方向的匀强电场,第1、Ⅳ象限内存在半径为L的圆形匀强磁场,磁场圆心在M(L,0)点,磁场方向垂直于坐标平面向外.一带正电粒子从第lll象限中的Q(-2L,-L)点以速度v0沿x轴正方向射出,恰好从坐标原点O进入磁场,从P(2L,0)点射出磁场.不计粒子重力,求:
(1)粒子到达O点时的速度
(2)电场强度与磁感应强度大小之比.
分析:(1)带电粒子在电场中做类平抛运动,水平方向做匀速直线运动,竖直方向做初速度为零的匀加速直线运动,根据运动学公式,可求解粒子到达O点时的速度.
(2)带电粒子进入磁场后做匀速圆周运动,由洛伦兹力提供向心力.对两过程,由牛顿运动定律可得出关于电场强度和磁感应强度的表达式,则可求得二者的比值;
(2)带电粒子进入磁场后做匀速圆周运动,由洛伦兹力提供向心力.对两过程,由牛顿运动定律可得出关于电场强度和磁感应强度的表达式,则可求得二者的比值;
解答: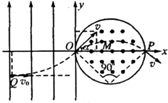 解:(1)设粒子的质量和所带正电荷分别为m和q,粒子在电场中做类似平抛运动
解:(1)设粒子的质量和所带正电荷分别为m和q,粒子在电场中做类似平抛运动
x方向:做匀速直线运动,则有:2L=v0t ①
y方向:做初速度为零的匀加速直线运动,则有 L=
t ②
由①②得:vy=v0
设粒子到达0点时速度为v,方向与x轴夹角为α
则tanα=
=1,得:α=45°
v=
=
v0.
(2)在电场中,
y方向:由牛顿第二定律得:
qE=ma,得:a=
又L=
at2=
?
(
)2
得:E=
①
离子进入磁场做匀速圆周运动,则有
qvB=
由图中几何关系R=
L
则由上两式得:B=
=
=
②
由①②解得:
=
答:(1)粒子到达O点时的速度是
v0,方向与x轴夹角为45°斜向右下方.
(2)电场强度与磁感应强度大小之比v0:2.
 解:(1)设粒子的质量和所带正电荷分别为m和q,粒子在电场中做类似平抛运动
解:(1)设粒子的质量和所带正电荷分别为m和q,粒子在电场中做类似平抛运动x方向:做匀速直线运动,则有:2L=v0t ①
y方向:做初速度为零的匀加速直线运动,则有 L=
| vy |
| 2 |
由①②得:vy=v0
设粒子到达0点时速度为v,方向与x轴夹角为α
则tanα=
| vy |
| v0 |
v=
|
| 2 |
(2)在电场中,
y方向:由牛顿第二定律得:
qE=ma,得:a=
| qE |
| m |
又L=
| 1 |
| 2 |
| 1 |
| 2 |
| qE |
| m |
| 2L |
| v0 |
得:E=
m
| ||
| 2qL |
离子进入磁场做匀速圆周运动,则有
qvB=
| mv2 |
| R |
由图中几何关系R=
| 2 |
则由上两式得:B=
| mv |
| qR |
m?
| ||
q?
|
| mv0 |
| qL |
由①②解得:
| E |
| B |
| v 0 |
| 2 |
答:(1)粒子到达O点时的速度是
| 2 |
(2)电场强度与磁感应强度大小之比v0:2.
点评:带电粒子在匀强电场中运动时,要注意应用运动的合成和分解;而在磁场中运动时为匀速圆周运动,在解题时要注意应用好平抛和圆周运动的性质.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
 如图,在直角坐标系xOy平面内,虚线MN平行于y轴,N点坐标(-l,0),MN与y轴之间有沿y轴正方向的匀强电场,在第四象限的某区域有方向垂直于坐标平面的圆形有界匀强磁场(图中未画出).现有一质量为m、电荷量为e的电子,从虚线MN上的P点,以平行于x轴正方向的初速度v0射入电场,并从y轴上A点(0,0.5l)射出电场,射出时速度方向与y轴负方向成30°角,此后,电子做匀速直线运动,进入磁场并从圆形有界磁场边界上Q点
如图,在直角坐标系xOy平面内,虚线MN平行于y轴,N点坐标(-l,0),MN与y轴之间有沿y轴正方向的匀强电场,在第四象限的某区域有方向垂直于坐标平面的圆形有界匀强磁场(图中未画出).现有一质量为m、电荷量为e的电子,从虚线MN上的P点,以平行于x轴正方向的初速度v0射入电场,并从y轴上A点(0,0.5l)射出电场,射出时速度方向与y轴负方向成30°角,此后,电子做匀速直线运动,进入磁场并从圆形有界磁场边界上Q点 如图,在平面直角坐标系xOy内,第Ⅰ象限存在沿y轴负方向的匀强电场,第Ⅳ象限以ON为直径的半圆形区域内,存在垂直于坐标平面向外的匀强磁场,磁感应强度为B.一质量为m、电荷量为q的带正电的粒子,从y轴正半轴上y=h处的M点,以速度v0垂直于y轴射入电场,经x轴上x=2h处的P点进入磁场,最后以垂直于y轴的方向射出磁场.不计粒子重力.则电场强度大小E=
如图,在平面直角坐标系xOy内,第Ⅰ象限存在沿y轴负方向的匀强电场,第Ⅳ象限以ON为直径的半圆形区域内,存在垂直于坐标平面向外的匀强磁场,磁感应强度为B.一质量为m、电荷量为q的带正电的粒子,从y轴正半轴上y=h处的M点,以速度v0垂直于y轴射入电场,经x轴上x=2h处的P点进入磁场,最后以垂直于y轴的方向射出磁场.不计粒子重力.则电场强度大小E=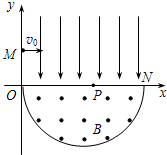 如图,在平面直角坐标系xOy内,第Ⅰ象限存在沿y轴负方向的匀强电场,第Ⅳ象限以ON为直径的半圆形区域内,存在垂直于坐标平面向外的匀强磁场,磁感应强度为B.一质量为m、电荷量为q的带正电的粒子,从y轴上y=h处的M点,以速度v0垂直于y轴射入电场,经x轴上x=2h处的P点进入磁场,最后以垂直于y轴的方向射出磁场.不计粒子重力.求
如图,在平面直角坐标系xOy内,第Ⅰ象限存在沿y轴负方向的匀强电场,第Ⅳ象限以ON为直径的半圆形区域内,存在垂直于坐标平面向外的匀强磁场,磁感应强度为B.一质量为m、电荷量为q的带正电的粒子,从y轴上y=h处的M点,以速度v0垂直于y轴射入电场,经x轴上x=2h处的P点进入磁场,最后以垂直于y轴的方向射出磁场.不计粒子重力.求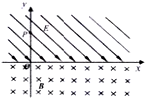 如图,在平面直角坐标系xoy中,x轴上方存在与y轴负方向成45°角的匀强电场,电场强度大小为E,在x轴下方存在垂直于坐标平面向里的匀强磁场,磁感应强度大小为B,现有一质量为m,电荷量为q的质子从y轴正半轴上的P点静止释放,经电场加速后以速度v0第一次进入磁场,不计粒子重力.求:
如图,在平面直角坐标系xoy中,x轴上方存在与y轴负方向成45°角的匀强电场,电场强度大小为E,在x轴下方存在垂直于坐标平面向里的匀强磁场,磁感应强度大小为B,现有一质量为m,电荷量为q的质子从y轴正半轴上的P点静止释放,经电场加速后以速度v0第一次进入磁场,不计粒子重力.求: