题目内容
 如图所示,边长为L的正方形PQMN(含边界)区域内有垂直纸面向外的匀强磁场,左侧有水平向右的匀强电场,场强大小为E,质量为m,电量为q的带正电粒子(不计重力)从O点静止释放,O、P、Q三点在同一水平线上,
如图所示,边长为L的正方形PQMN(含边界)区域内有垂直纸面向外的匀强磁场,左侧有水平向右的匀强电场,场强大小为E,质量为m,电量为q的带正电粒子(不计重力)从O点静止释放,O、P、Q三点在同一水平线上,OP=L,带电粒子恰好从M点离开磁场,求:
(1)磁感应强度B的大小;
(2)粒子从O到M的时间.
分析:(1)带电粒子在电场中做加速运动,在磁场中做运动圆周运动,根据动能定理及向心力公式列式,联立方程即可求解B;
(2)根据匀加速直线运动位移时间公式求出粒子在电场中运动的时间,根据粒子在匀强磁场中做匀速圆周运动的周期公式求出在磁场中运动的时间,两者之和即为总时间;
(2)根据匀加速直线运动位移时间公式求出粒子在电场中运动的时间,根据粒子在匀强磁场中做匀速圆周运动的周期公式求出在磁场中运动的时间,两者之和即为总时间;
解答:解:(1)设粒子运动到P点时的速度大小为v,则有
qEL=
mv2
粒子在匀强磁场中做匀速圆周运动,半径r=L,
Bqv=m
解得:B=
(2)设粒子在匀强电场中运动的时间为t1,有:
L=
at12=
t12
解得:t1=
粒子在匀强磁场中做匀速圆周运动的周期T=
,运动时间t2=
,
所以t2=
所以粒子从O点运动到M点经历的时间t=t1+t2=
答:(1)磁感应强度B的大小为
;
(2)粒子从O到M的时间为
.
qEL=
| 1 |
| 2 |
粒子在匀强磁场中做匀速圆周运动,半径r=L,
Bqv=m
| v2 |
| r |
解得:B=
|
(2)设粒子在匀强电场中运动的时间为t1,有:
L=
| 1 |
| 2 |
| qE |
| 2m |
解得:t1=
|
粒子在匀强磁场中做匀速圆周运动的周期T=
| 2πm |
| qB |
| T |
| 4 |
所以t2=
| π |
| 2 |
|
所以粒子从O点运动到M点经历的时间t=t1+t2=
| 4+π |
| 4 |
|
答:(1)磁感应强度B的大小为
|
(2)粒子从O到M的时间为
| 4+π |
| 4 |
|
点评:本题是带电粒子在组合场中运动的问题,知道带电粒子在电场中做匀加速运动,在磁场中做匀速圆周运动,并能结合几何关系求解,难度适中.

练习册系列答案
相关题目
 如图所示,边长为L的正方形区域abcd内存在着匀强电场.电量为q、动能为Ek的带电粒子从a点沿ab方向进入电场,不计带电粒子的重力.
如图所示,边长为L的正方形区域abcd内存在着匀强电场.电量为q、动能为Ek的带电粒子从a点沿ab方向进入电场,不计带电粒子的重力. 如图所示,边长为L的正方形线图abcd匝数为n、电阻为r,外电路的电阻为R,线圈位于磁感应强度为B的匀强磁场中,若线圈从图示位置开始,以角速度ω绕OO′轴匀速转动,则以下判断中正确的是( )
如图所示,边长为L的正方形线图abcd匝数为n、电阻为r,外电路的电阻为R,线圈位于磁感应强度为B的匀强磁场中,若线圈从图示位置开始,以角速度ω绕OO′轴匀速转动,则以下判断中正确的是( )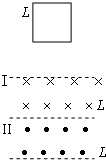 如图所示,边长为L的正方形导线框底边水平,且平行于正下方的磁场边界,正下方的匀强磁场宽度均为L,磁感强度等值反向,两磁场区域紧邻.当线框底边进入磁场I区域时,导线框恰好做匀速运动,这时导线框的电功率为P.则当导线框底边刚进入磁场II区域时,下列结论正确的是( )
如图所示,边长为L的正方形导线框底边水平,且平行于正下方的磁场边界,正下方的匀强磁场宽度均为L,磁感强度等值反向,两磁场区域紧邻.当线框底边进入磁场I区域时,导线框恰好做匀速运动,这时导线框的电功率为P.则当导线框底边刚进入磁场II区域时,下列结论正确的是( )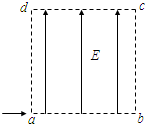 如图所示,边长为L的正方形区域abcd内存在着匀强电场,一个质量为m、电量为q、初速度为v0的带电
如图所示,边长为L的正方形区域abcd内存在着匀强电场,一个质量为m、电量为q、初速度为v0的带电 如图所示,边长为L的正方形闭合线框,在磁感应强度为B的匀强磁场中,以一条边为轴,以角速度ω匀速转动,转轴与B垂直,线圈总电阻为R,导线电阻不计.下列说法中正确的是( )
如图所示,边长为L的正方形闭合线框,在磁感应强度为B的匀强磁场中,以一条边为轴,以角速度ω匀速转动,转轴与B垂直,线圈总电阻为R,导线电阻不计.下列说法中正确的是( )