题目内容
4. A、B两球在光滑水平面上沿一直线相向运动,已知B球的质量是A球质量的4倍,碰撞前A球速度大小为vA=v,B球速度大小vB=$\frac{2}{3}$v,若碰后B球速度减小为$\frac{1}{3}$v但方向不变,则碰撞前后系统的总动量不变(选填“不变”、“增大”或“减小”),碰后A球的速度大小vA=$\frac{1}{3}v$.
A、B两球在光滑水平面上沿一直线相向运动,已知B球的质量是A球质量的4倍,碰撞前A球速度大小为vA=v,B球速度大小vB=$\frac{2}{3}$v,若碰后B球速度减小为$\frac{1}{3}$v但方向不变,则碰撞前后系统的总动量不变(选填“不变”、“增大”或“减小”),碰后A球的速度大小vA=$\frac{1}{3}v$.
分析 碰撞过程中A、B两球组成的系统动量守恒,结合动量守恒定律求出碰后A的速度大小.
解答 解:碰撞过程中,系统所受的外力之和为零,系统动量守恒,即碰撞前后系统的总动量不变.
规定向右为正方向,根据动量守恒定律得:
mAvA+mBvB=mAvA′+mBvB′,
即:${m}_{A}v-{m}_{B}•\frac{2}{3}v={m}_{A}{v}_{A}′-{m}_{B}•\frac{1}{3}v$,
又mB=4mA,
解得碰后A的速度vA′=$-\frac{1}{3}v$,负号表示方向.
故答案为:不变,$\frac{1}{3}$v.
点评 本题考查了动量守恒定律的基本运用,运用动量守恒定律解题时,要注意速度的方向,与规定正方向相同,取正值,与规定正方向相反,取负值.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
16.下列说法正确的是( )
| A. | 亚里士多德首先提出了惯性的概念 | |
| B. | 牛顿的三条运动定律是研究动力学问题的基石,都能通过现代的实验手段直接验证 | |
| C. | 紫外线照射到金属锌板表面时能够发生光电效应,则当增大紫外线的强度时,从锌板表面逸出的光电子的最大初动能也随之增大 | |
| D. | 汤姆孙发现了电子,查德威克发现了中子,卢瑟福发现了质子,比结合能越大的原子核越稳定 |
13.物块1、2的质量分别是m1=4kg和m2=1kg,它们具有的动能分别为E1和E2,且E1+E2=100J.若两物块沿同一直线相向运动发生碰撞,并黏在一起,欲使碰撞中损失的机械能最大,则E1和E2的值应该分别是( )
| A. | E1=E2=50 J | B. | E1=20 J,E2=80 J | C. | E1=1 J,E2=99 J | D. | E1=90 J,E2=10 J |
17. 如图所示,质量为 M 的楔形物体静止在光滑的水平地面上,其 斜面光滑且足够长,与水平方向的夹角为θ.一个质量为 m 的小 物块从斜面底端沿斜面向上以初速度 v0开始运动.当小物块沿斜面向上运动到最高点时,速度大小为 v,距地面高度为 h,则下列关系式中正确的是( )
如图所示,质量为 M 的楔形物体静止在光滑的水平地面上,其 斜面光滑且足够长,与水平方向的夹角为θ.一个质量为 m 的小 物块从斜面底端沿斜面向上以初速度 v0开始运动.当小物块沿斜面向上运动到最高点时,速度大小为 v,距地面高度为 h,则下列关系式中正确的是( )
 如图所示,质量为 M 的楔形物体静止在光滑的水平地面上,其 斜面光滑且足够长,与水平方向的夹角为θ.一个质量为 m 的小 物块从斜面底端沿斜面向上以初速度 v0开始运动.当小物块沿斜面向上运动到最高点时,速度大小为 v,距地面高度为 h,则下列关系式中正确的是( )
如图所示,质量为 M 的楔形物体静止在光滑的水平地面上,其 斜面光滑且足够长,与水平方向的夹角为θ.一个质量为 m 的小 物块从斜面底端沿斜面向上以初速度 v0开始运动.当小物块沿斜面向上运动到最高点时,速度大小为 v,距地面高度为 h,则下列关系式中正确的是( )| A. | mv0=(m+M )v | B. | mv0cosθ=(m+M )v | ||
| C. | mgh+$\frac{1}{2}$(m+M)v2=$\frac{1}{2}$mv02cos2θ | D. | mgh=$\frac{1}{2}$mv02-$\frac{1}{2}$mv2 |
 如图所示,长L的轻杆两端分别固定有质量均为m的A、B两小铁球,杆的三等分点O处有光滑的水平固定转轴,使轻杆可绕转轴在竖直面内无摩擦转动.用手将该装置固定在杆恰好水平的位置,然后由静止释放.重力加速度为g.求(结论可以用根号表示):
如图所示,长L的轻杆两端分别固定有质量均为m的A、B两小铁球,杆的三等分点O处有光滑的水平固定转轴,使轻杆可绕转轴在竖直面内无摩擦转动.用手将该装置固定在杆恰好水平的位置,然后由静止释放.重力加速度为g.求(结论可以用根号表示):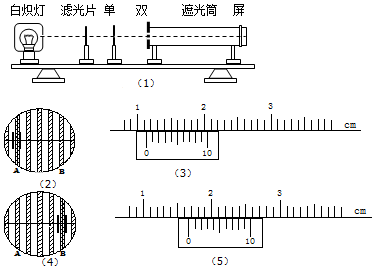 利用图中装置研究双缝干涉现象:
利用图中装置研究双缝干涉现象: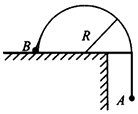 如图所示是一个横截面为半圆、半径为R的光滑柱面,一根不可伸长的细线两端分别系着物体A、B,且mA=2mB,由图示位置从静止开始释放A物体,当物体B达到圆柱顶点时,
如图所示是一个横截面为半圆、半径为R的光滑柱面,一根不可伸长的细线两端分别系着物体A、B,且mA=2mB,由图示位置从静止开始释放A物体,当物体B达到圆柱顶点时,