题目内容
1.人造地球卫星绕地球做匀速圆周运动,假如卫星的线速度减小到原来的$\frac{1}{2}$,卫星仍然做匀速圆周运动,则( )| A. | 卫星的向心加速度减小到原来的$\frac{1}{4}$ | B. | 卫星的周期增大到原来的8倍 | ||
| C. | 卫星的角速度减小到原来的$\frac{1}{2}$ | D. | 卫星的周期增大到原来的2倍 |
分析 根据万有引力提供向心力,列式得出向心加速度、周期、角速度与轨道半径的关系,再得出这些物理量的变化.
解答 解:卫星绕地做匀速圆周运动,根据万有引力提供向心力,得:
G$\frac{Mm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$=ma=m$\frac{4{π}^{2}}{{T}^{2}}$r=mω2r,得 v=$\sqrt{\frac{GM}{r}}$,a=$\frac{GM}{{r}^{2}}$,T=2π$\sqrt{\frac{{r}^{3}}{GM}}$,ω=$\sqrt{\frac{GM}{{r}^{3}}}$
由v=$\sqrt{\frac{GM}{r}}$可得,当卫星的线速度减小到原来的$\frac{1}{2}$时,轨道半径增大为原来的4倍.
由a=$\frac{GM}{{r}^{2}}$,得知,向心加速度减小到原来的$\frac{1}{16}$.
由T=2π$\sqrt{\frac{{r}^{3}}{GM}}$,得知,卫星的周期增大到原来的8倍.
由ω=$\sqrt{\frac{GM}{{r}^{3}}}$得知,卫星的角速度减小到原来的$\frac{1}{8}$.故ACD错误,B正确.
故选:B
点评 解决本题的关键掌握万有引力提供向心力这一思路,知道线速度、角速度、周期、加速度与轨道半径的关系,要能熟练运用比例法.

练习册系列答案
相关题目
16.下列哪种情况下,物体会做离心运动( )
| A. | 合力大于向心力 | B. | 合力小于向心力 | C. | 合力等于向心力 | D. | 与受力无关 |
6.从地面上以20m/s的初速度竖直向上抛一小球,不计空气阻力,取g=l0m/s2.以下判断正确的是( )
| A. | 小球到达最大高度时的速度为0 | B. | 小球到达最大高度时的加速度为0 | ||
| C. | 小球上升的最大高度为30m | D. | 小球上升阶段所用的时间为2s |
10. 如图是观察布朗运动时每隔30s,记录1次的微粒位置连线图,开始时微粒在位置1,以后的位置依次是2、3、4、…,由此图得到的下列结论中正确的是( )
如图是观察布朗运动时每隔30s,记录1次的微粒位置连线图,开始时微粒在位置1,以后的位置依次是2、3、4、…,由此图得到的下列结论中正确的是( )
 如图是观察布朗运动时每隔30s,记录1次的微粒位置连线图,开始时微粒在位置1,以后的位置依次是2、3、4、…,由此图得到的下列结论中正确的是( )
如图是观察布朗运动时每隔30s,记录1次的微粒位置连线图,开始时微粒在位置1,以后的位置依次是2、3、4、…,由此图得到的下列结论中正确的是( )| A. | 此图反映了观察时间内微粒的运动轨迹 | |
| B. | 此图只是间接地反映了液体分子运动是无规则运动 | |
| C. | 若在第75s再观察一次,微粒应处于位置3和位置4连线的中点 | |
| D. | 微粒在从位置7到位置8的这30s,内运动得最快 |
 2014年10月8日,月全食带来的“红月亮”亮相天空,引起人们对月球的关注.我国发射的“嫦娥三号”探月卫星沿近似于圆形的轨道绕月飞行.设卫星距月球表面的高度为h,做匀速圆周运动的周期为T.已知月球半径为R,引力常量为G.试求:
2014年10月8日,月全食带来的“红月亮”亮相天空,引起人们对月球的关注.我国发射的“嫦娥三号”探月卫星沿近似于圆形的轨道绕月飞行.设卫星距月球表面的高度为h,做匀速圆周运动的周期为T.已知月球半径为R,引力常量为G.试求:
 某实验小组同学用如图所示装置探究“物体加速度与力、质量的关系”.
某实验小组同学用如图所示装置探究“物体加速度与力、质量的关系”.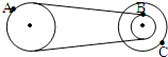 如图所示的皮带传动装置中,右边两轮粘在一起且同轴,A、B、C三点均是各轮边缘上的一点,半径RA=RC=2RB,皮带不打滑,则:线速度vA:vB:vC=1:1:2;向心加速度aA:aB:aC=1:2:4.
如图所示的皮带传动装置中,右边两轮粘在一起且同轴,A、B、C三点均是各轮边缘上的一点,半径RA=RC=2RB,皮带不打滑,则:线速度vA:vB:vC=1:1:2;向心加速度aA:aB:aC=1:2:4.