题目内容
一个初速度为零的电子通过电压为U=4500V的电场加速后，从C点沿水平方向飞入电场强度为E=1.5×105V/m的匀强电场中，到达该电场中另一点D时，电子的速度方向与电场强度方向的夹角正好是120°，如图所示．试求C、D两点沿电场强度方向的距离y．
【答案】分析：对电子的加速过程运用动能定理得到C点速度，再结合D点速度方向得到y方向的分速度，根据牛顿第二定律和运动学公式列式求解．
解答：解：电子加速过程，由动能定理得到
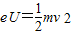
解得
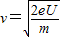
在竖直方向：vy=vtan30°=at，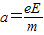
解得：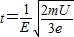
CD两点沿场强方向的距离
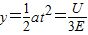
代入数据解得
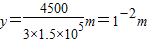
即C、D两点沿电场强度方向的距离y为0.01m．
点评：本题关键要将C到D的类平抛运动正交分解为水平和竖直方向的直线运动分析求解．
解答：解：电子加速过程，由动能定理得到
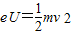
解得
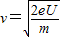
在竖直方向：vy=vtan30°=at，
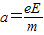
解得：
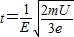
CD两点沿场强方向的距离
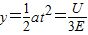
代入数据解得
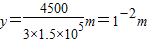
即C、D两点沿电场强度方向的距离y为0.01m．
点评：本题关键要将C到D的类平抛运动正交分解为水平和竖直方向的直线运动分析求解．
练习册系列答案
阅读快车系列答案
相关题目
一个初速度为零的电子在U1=45V的电压作用下得到一定速度后垂直于平行板间的匀强电场飞入两板间的中央，如图所示．若平行板间的距离d=1cm，板长l=1.5cm，电子的电荷量e=1.6×10 -19C，电子的质量m=9×10 -31kg，求：
（2011?兴宁区模拟）M、N是某电场中一条电场线上的两点，若在M点释放一个初速度为零的电子，电子仅受电场力作用，并沿电场线由M点运动到N点，其电势能随位移变化的关系如图所示，则下列说法正确的是（ ）
M、N是某电场中一条电场线上的两点，若在M点释放一个初速度为零的电子，电子仅受电场力作用，并沿电场线由M点运动到N点，其电势能随位移变化的关系如图所示，则下列说法正确的是（ ）| A、电子在N点的动能小于在M点的动能 | B、该电场不可能是匀强电场 | C、该电子运动的加速度越来越小 | D、电子运动的轨迹为曲线 |
M、N是某电场中一条电场线上的两点，若在M点释放一个初速度为零的电子，电子仅受电场力作用，并沿电场线由M点运动到N点，其电势能EP随位移x变化的关系如图所示，则下列说法正确的是（ ）| A、电子在N点的动能小于在M点的动能 | B、该电场有可能是匀强电场 | C、该电子运动的加速度越来越小 | D、电子运动的轨迹为曲线 |
一个初速度为零的电子通过电压为U的电场加速后，从C点沿水平方向飞入电场强度为E的匀强电场中，到达该电场中另一点D时，电子的速度方向与电场强度方向的夹角正好是120°，如图所示．试求C、D两点沿电场强度方向的距离y．