题目内容
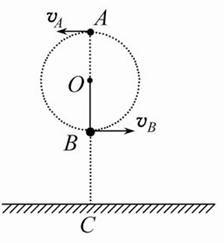
如图所示,有一长为L的细线,细线的一端固定在O点,另一端拴一质量为m的小球,现使小球恰好能在竖直面内做完整的圆周运动。已知水平地面上的C点位于O点正下方,且到O点的距离为1.9L。不计空气阻力。
(1)求小球通过最高点A时的速度vA;
(2)若小球通过最低点B时,细线对小球的拉力FT恰好为小球重力的6倍,且小球经过B点的瞬间让细线断裂,求小球落地点到C点的距离。
【解析】(1)小球恰好能做完整的圆周运动,则小球通过A点时细线的拉力刚好为零,根据向心力公式有:
mg=![]() (2分)
(2分)
解得:![]() 。 (2分)
。 (2分)
(2)小球在B点时根据牛顿第二定律有:
FT-mg=m![]() (2分)
(2分)
其中FT=6mg
解得小球在B点的速度大小为vB=![]() (2分)
(2分)
细线断裂后,小球从B点开始做平抛运动,则由平抛运动的规律得:
竖直方向上1.9L-L=![]() (2分)
(2分)
水平方向上x=vBt (2分)
解得:x=3L (2分)
即小球落地点到C点的距离为3L。
答案:(1)![]() (2)3L
(2)3L

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案 如图所示,有一长为L的细线,细线的一端固定在O点,另一端拴一质量为m的小球,现使小球恰好能在竖直面内做完整的圆周运动.已知水平地面上的C点位于O点正下方,且到O点的距离为1.9L.不计空气阻力.求:
如图所示,有一长为L的细线,细线的一端固定在O点,另一端拴一质量为m的小球,现使小球恰好能在竖直面内做完整的圆周运动.已知水平地面上的C点位于O点正下方,且到O点的距离为1.9L.不计空气阻力.求: 如图所示,有一长为L右端开口的圆柱形气缸,一个质量不计的薄活塞封闭一定质量的理想气体,开始时活塞处在离左端
如图所示,有一长为L右端开口的圆柱形气缸,一个质量不计的薄活塞封闭一定质量的理想气体,开始时活塞处在离左端 如图所示,有一长为l=1.75m、质量为mB=1.6kg的长木板B放在光滑水平面上,长木板的左端通过一条拉直的细线连接在墙上;另有一个物块A,质量为mA=0.4kg,放在木板左端,在水平恒力F=1.2N的作用下由静止幵始向右匀加速运动.当物块A滑过x=0.5m的距离时,剪断细线,之后物块A在恒力作用下继续向右运动.已知物块A与长木板B之间的动摩擦因数为μ=0.2,物块A的大小不计.求:
如图所示,有一长为l=1.75m、质量为mB=1.6kg的长木板B放在光滑水平面上,长木板的左端通过一条拉直的细线连接在墙上;另有一个物块A,质量为mA=0.4kg,放在木板左端,在水平恒力F=1.2N的作用下由静止幵始向右匀加速运动.当物块A滑过x=0.5m的距离时,剪断细线,之后物块A在恒力作用下继续向右运动.已知物块A与长木板B之间的动摩擦因数为μ=0.2,物块A的大小不计.求: 如图所示,有一长为L质量为M的木板,一端用铰链固定在水平地面上,另一端靠在直墙上,木板与地面夹角为θ,设木板与竖直平面AO之间没有摩擦.在木板的上端放一个质量为m的物体,物体与木板间动摩擦因数为μ,试回答:
如图所示,有一长为L质量为M的木板,一端用铰链固定在水平地面上,另一端靠在直墙上,木板与地面夹角为θ,设木板与竖直平面AO之间没有摩擦.在木板的上端放一个质量为m的物体,物体与木板间动摩擦因数为μ,试回答: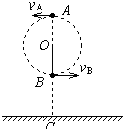 如图所示,有一长为L=0.9m的细线,细线的一端固定在O点,另一端拴一质量为m的小球,现使小球恰好能在竖直面内做完整的圆周运动.已知水平地面上的C点位于O点正下方,且到O点的距离为h=1.9m,不计空气阻力.(g取10m/s2)
如图所示,有一长为L=0.9m的细线,细线的一端固定在O点,另一端拴一质量为m的小球,现使小球恰好能在竖直面内做完整的圆周运动.已知水平地面上的C点位于O点正下方,且到O点的距离为h=1.9m,不计空气阻力.(g取10m/s2)