题目内容
16.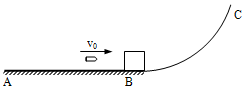 水平轨道AB,在B点处与半径R=100m的光滑弧形轨道BC相切,一个质量为M=1.0kg的木块以v0=1m/s的水平速度从B点冲上弧形轨道,如图所示.已知木块与该水平轨道AB的动摩擦因数μ=0.5(g取10m/s2).试求:
水平轨道AB,在B点处与半径R=100m的光滑弧形轨道BC相切,一个质量为M=1.0kg的木块以v0=1m/s的水平速度从B点冲上弧形轨道,如图所示.已知木块与该水平轨道AB的动摩擦因数μ=0.5(g取10m/s2).试求:(1)木块从冲上弧形轨道的高度;
(2)木块在水平面上运动的时间;
(3)木块在圆弧轨道上运动的时间.
分析 (1)木块冲上光滑弧形轨道的过程中,只有重力做功,机械能守恒,由机械能守恒定律求木块从冲上弧形轨道的高度;
(2)木块在水平面上做匀减速运动,由牛顿第二定律和速度时间公式结合求时间;
(3)木块在圆弧轨道上做简谐运动,类似于单摆,根据单摆的周期公式求木块在圆弧轨道上运动的时间.
解答 解:(1)木块沿光滑圆弧轨道上升的过程,由机械能守恒定律有
$\frac{1}{2}$Mv02=Mgh
得 h=$\frac{{v}_{0}^{2}}{2g}$=$\frac{{1}^{2}}{20}$m=0.05m
(2)根据机械能守恒知,木块滑回水平面时速度大小为 v=v0=1m/s
加速度大小为 a=$\frac{μmg}{m}$=μg
由v=at得 t=$\frac{{v}_{0}}{μg}$=$\frac{1}{0.5×10}$=0.2s
(3)因为h<<R,所以木块在BC面上一个往返运动的时间为等效单摆运动的半个周期,为 t′=$π\sqrt{\frac{R}{g}}$=3.14×$\sqrt{\frac{100}{10}}$≈10.0s.
答:
(1)木块从冲上弧形轨道的高度是0.05m.
(2)木块在水平面上运动的时间是0.2s.
(3)木块在圆弧轨道上运动的时间是10s.
点评 解决本题的关键是运用等效法研究木块圆弧轨道上的运动情况,知道该运动可等效为单摆,等效单摆的摆长等于圆弧的半径.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
1.下列说法正确的是( )
| A. | 机械波在传播的过程中,每个质点的起振方向均相同 | |
| B. | 机械波从一种介质传入另一种介质时,波长不变 | |
| C. | 泊松亮斑的形成是由于光具有波动性 | |
| D. | 薄膜干涉是薄膜前后表面反射光的干涉现象 | |
| E. | 用单摆测当地的重力加速度的实验中,测量摆长时,忘记测量小球的直径,会导致重力加速度测量结果偏大 |
2.物体受到以下各组力作用时,可能处于平衡状态的是( )
| A. | 2N,5N | B. | 3N,6N,8N | ||
| C. | 1N,6N,8N,14N | D. | 2N,5N,7N,15N,31N |
11. 如图所示,一理想变压器原副线圈的匝数比为1:2;副线圈电路中接有灯泡,灯泡的额定电压为220V,额定功率为22W;原线圈电路中接有电压表和电流表.现闭合开关,灯泡正常发光.若用U和I分别表示此时电压表和电流表的读数,则( )
如图所示,一理想变压器原副线圈的匝数比为1:2;副线圈电路中接有灯泡,灯泡的额定电压为220V,额定功率为22W;原线圈电路中接有电压表和电流表.现闭合开关,灯泡正常发光.若用U和I分别表示此时电压表和电流表的读数,则( )
 如图所示,一理想变压器原副线圈的匝数比为1:2;副线圈电路中接有灯泡,灯泡的额定电压为220V,额定功率为22W;原线圈电路中接有电压表和电流表.现闭合开关,灯泡正常发光.若用U和I分别表示此时电压表和电流表的读数,则( )
如图所示,一理想变压器原副线圈的匝数比为1:2;副线圈电路中接有灯泡,灯泡的额定电压为220V,额定功率为22W;原线圈电路中接有电压表和电流表.现闭合开关,灯泡正常发光.若用U和I分别表示此时电压表和电流表的读数,则( )| A. | U=110$\sqrt{2}$V,I=$\frac{\sqrt{2}}{5}$A | B. | U=110V,I=0.05A | C. | U=110$\sqrt{2}$V,I=0.2A | D. | U=110V,I=0.2A |
8. 2009年12月26日正式运营的武汉至广州高铁客运新干线是目前世界上第一条平均时速高达360km、里程最长的无砟轨道客运专线,武汉至广州的运行时间由原来的10个多小时缩短至2小时50分左右.虽然运行在专线上的“和谐号”动车组最高运行时速近400km,但由于动车组加速均匀,乘客不会感受到强烈的推背感.假定一动车组某次进站前、后一段时间内的速率-时间图象如图所示.下列说法正确的是( )
2009年12月26日正式运营的武汉至广州高铁客运新干线是目前世界上第一条平均时速高达360km、里程最长的无砟轨道客运专线,武汉至广州的运行时间由原来的10个多小时缩短至2小时50分左右.虽然运行在专线上的“和谐号”动车组最高运行时速近400km,但由于动车组加速均匀,乘客不会感受到强烈的推背感.假定一动车组某次进站前、后一段时间内的速率-时间图象如图所示.下列说法正确的是( )
 2009年12月26日正式运营的武汉至广州高铁客运新干线是目前世界上第一条平均时速高达360km、里程最长的无砟轨道客运专线,武汉至广州的运行时间由原来的10个多小时缩短至2小时50分左右.虽然运行在专线上的“和谐号”动车组最高运行时速近400km,但由于动车组加速均匀,乘客不会感受到强烈的推背感.假定一动车组某次进站前、后一段时间内的速率-时间图象如图所示.下列说法正确的是( )
2009年12月26日正式运营的武汉至广州高铁客运新干线是目前世界上第一条平均时速高达360km、里程最长的无砟轨道客运专线,武汉至广州的运行时间由原来的10个多小时缩短至2小时50分左右.虽然运行在专线上的“和谐号”动车组最高运行时速近400km,但由于动车组加速均匀,乘客不会感受到强烈的推背感.假定一动车组某次进站前、后一段时间内的速率-时间图象如图所示.下列说法正确的是( )| A. | 武汉至广州距离接近1 000 km | |
| B. | 武汉至广州距离接近1 200 km | |
| C. | 由图象可知,因本次停站增加的运行时间为11 min | |
| D. | 由图知,在车组做变速运动时,乘客在水平方向受到的合力不超过其重力的0.02倍 |
6. 如图所示,质量为m的木块在大小为F、方向与水平面成θ角斜向左下的恒力作用下,在水平地面上向左做匀速直线运动.木块与地面间的动摩擦因数为μ,那么木块受到的滑动摩擦力大小为( )
如图所示,质量为m的木块在大小为F、方向与水平面成θ角斜向左下的恒力作用下,在水平地面上向左做匀速直线运动.木块与地面间的动摩擦因数为μ,那么木块受到的滑动摩擦力大小为( )
 如图所示,质量为m的木块在大小为F、方向与水平面成θ角斜向左下的恒力作用下,在水平地面上向左做匀速直线运动.木块与地面间的动摩擦因数为μ,那么木块受到的滑动摩擦力大小为( )
如图所示,质量为m的木块在大小为F、方向与水平面成θ角斜向左下的恒力作用下,在水平地面上向左做匀速直线运动.木块与地面间的动摩擦因数为μ,那么木块受到的滑动摩擦力大小为( )| A. | μmg | B. | μ (mg-Fsin θ) | C. | μ(mg+Fsin θ) | D. | Fcos θ |
 如图所示,光滑固定细杆与水平方向夹角为53°,轻质弹簧一端固定在O点,另一端连接一个中央带孔(孔径略大于杆的直径)的小球,小球套在细杆上.现将小球拉至弹簧处于水平位置并由静止释放,测得下滑过程中小球的机械能先增大后减小,当小球的动能最大时弹簧的弹性势能恰好与初始时相同.已知小球质量为m,O点到杆的距离为l,重力加速度为g,弹簧始终处于弹性限度内,sin53°=0.8,cos53°=0.6.由以上条件可求出:小球的最大速度为$\sqrt{\frac{12gl}{5}}$,加速过程的最大加速度为$\frac{8}{5}g$,弹簧劲度系数的最大可能值为$\frac{16mg}{3l}$.
如图所示,光滑固定细杆与水平方向夹角为53°,轻质弹簧一端固定在O点,另一端连接一个中央带孔(孔径略大于杆的直径)的小球,小球套在细杆上.现将小球拉至弹簧处于水平位置并由静止释放,测得下滑过程中小球的机械能先增大后减小,当小球的动能最大时弹簧的弹性势能恰好与初始时相同.已知小球质量为m,O点到杆的距离为l,重力加速度为g,弹簧始终处于弹性限度内,sin53°=0.8,cos53°=0.6.由以上条件可求出:小球的最大速度为$\sqrt{\frac{12gl}{5}}$,加速过程的最大加速度为$\frac{8}{5}g$,弹簧劲度系数的最大可能值为$\frac{16mg}{3l}$.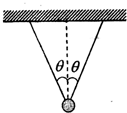 如图所示,两条等长的细绳的一端固定于水平横梁的两点,另一端悬吊一重物,绳与竖直方向的夹角θ可取不同的值,此时绳的张力为F1.如图,突然剪断其中一根绳,则在剪断瞬间,另一根绳的张力为F2,比较F1和F2的大小,我们作出的判定是F2>F1.
如图所示,两条等长的细绳的一端固定于水平横梁的两点,另一端悬吊一重物,绳与竖直方向的夹角θ可取不同的值,此时绳的张力为F1.如图,突然剪断其中一根绳,则在剪断瞬间,另一根绳的张力为F2,比较F1和F2的大小,我们作出的判定是F2>F1.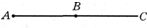 如图所示,B为直线AC的中点,质点甲从A点由静止出发做匀加速运动,到达B点时的速度为v,则它到达C点时的速度大小为$\sqrt{2}v$;若质点乙也从A点由静止出发,在AC间做简谐运动,到达B点时的速度也为v,则甲、乙从A点到B点所用的时间之比为$\sqrt{2}$:1.
如图所示,B为直线AC的中点,质点甲从A点由静止出发做匀加速运动,到达B点时的速度为v,则它到达C点时的速度大小为$\sqrt{2}v$;若质点乙也从A点由静止出发,在AC间做简谐运动,到达B点时的速度也为v,则甲、乙从A点到B点所用的时间之比为$\sqrt{2}$:1.