题目内容
4. 在研究平抛运动的实验中,用一张印有方格的纸记录运动的轨迹,小方格的边长为L,若小球在平抛运动中的几个位置如图中a、b、c、d所示,则:
在研究平抛运动的实验中,用一张印有方格的纸记录运动的轨迹,小方格的边长为L,若小球在平抛运动中的几个位置如图中a、b、c、d所示,则:(1)小球做平抛运动的初速度的计算式是什么(用L、g表示)?
(2)a点是小球抛出点的位置吗?为什么?
(3)b点的速度是多少(用L、g表示)?
分析 根据竖直方向上连续相等时间内的位移之差是一恒量求出相等的时间间隔,结合水平位移和时间间隔求出初速度的表达式.
根据竖直方向上某段时间内的平均速度等于中间时刻的瞬时速度求出b点的竖直分数的,结合速度时间公式求出a点的竖直分速度,判断a点是否是抛出点的位置.
根据b点竖直分速度和初速度,结合平行四边形定则求出b点的速度.
解答 解:(1)在竖直方向上,根据△y=L=gT2得:T=$\sqrt{\frac{L}{g}}$,
则平抛运动的初速度为:${v}_{0}=\frac{2L}{T}=2\sqrt{gL}$.
(2)b点的竖直分速度为:${v}_{yb}=\frac{3L}{2T}=\frac{3}{2}\sqrt{gL}$,
则a点的竖直分速度为:${v}_{ya}={v}_{yb}-gT=\frac{1}{2}\sqrt{gL}≠0$,
可知a点不是小球抛出点的位置.
(3)根据平行四边形定则知,b点的速度为:
${v}_{b}=\sqrt{{{v}_{0}}^{2}+{{v}_{yb}}^{2}}$=$\sqrt{4gL+\frac{9gL}{4}}=\frac{5}{2}\sqrt{gL}$.
答:(1)(1)小球做平抛运动的初速度的计算式是${v}_{0}=2\sqrt{gL}$
(2)a点不是小球抛出点的位置.
(3)b点的速度是$\frac{5}{2}\sqrt{gL}$.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式和推论灵活求解.

练习册系列答案
相关题目
14. 如图所示,两辆质量相同的平板小车a、b成一直线排列,静止在光滑水平地面上,原来静止在a车上的一个小孩跳到b,接着又立即从b跳回a车,他跳回a车并相对a车保持静止,此后( )
如图所示,两辆质量相同的平板小车a、b成一直线排列,静止在光滑水平地面上,原来静止在a车上的一个小孩跳到b,接着又立即从b跳回a车,他跳回a车并相对a车保持静止,此后( )
 如图所示,两辆质量相同的平板小车a、b成一直线排列,静止在光滑水平地面上,原来静止在a车上的一个小孩跳到b,接着又立即从b跳回a车,他跳回a车并相对a车保持静止,此后( )
如图所示,两辆质量相同的平板小车a、b成一直线排列,静止在光滑水平地面上,原来静止在a车上的一个小孩跳到b,接着又立即从b跳回a车,他跳回a车并相对a车保持静止,此后( )| A. | a、b两车的速率相等 | B. | a车的速率大于b车的速率 | ||
| C. | a车的速率小于b车的速率 | D. | a、b两车均静止 |
12.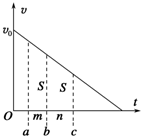 一个物体以初速度v0沿光滑斜面向上运动,其速度v随时间t变化的规律如图所示,在连续两段时间m和n内对应面积均为S,设经过b时刻的加速度和速度分别为a和vb,则( )
一个物体以初速度v0沿光滑斜面向上运动,其速度v随时间t变化的规律如图所示,在连续两段时间m和n内对应面积均为S,设经过b时刻的加速度和速度分别为a和vb,则( )
 一个物体以初速度v0沿光滑斜面向上运动,其速度v随时间t变化的规律如图所示,在连续两段时间m和n内对应面积均为S,设经过b时刻的加速度和速度分别为a和vb,则( )
一个物体以初速度v0沿光滑斜面向上运动,其速度v随时间t变化的规律如图所示,在连续两段时间m和n内对应面积均为S,设经过b时刻的加速度和速度分别为a和vb,则( )| A. | a=$\frac{2(m+n)S}{(m-n)mn}$ | B. | a=$\frac{2(m-n)S}{(m+n)mn}$ | C. | vb=$\frac{(m+n)S}{mn}$ | D. | vb=$\frac{({m}^{2}+{n}^{2})S}{mn}$ |
9.对于匀速圆周运动的物体,下列说法中正确的是( )
| A. | 线速度不变 | B. | 角速度不变 | C. | 周期不变 | D. | 向心加速度不变 |
16. 如图所示,一细束a光和一细束b光平行射到同一个三棱镜上,经折射后交于光屏上的同一个点M,若用n1和n2分别表示三棱镜对a光和b光的折射率,用v1和v2分别表示a光和b光在三棱镜中的光速,用λ1和λ2分别表示a光和b光在三棱镜中的波长,下列说法正确的是( )
如图所示,一细束a光和一细束b光平行射到同一个三棱镜上,经折射后交于光屏上的同一个点M,若用n1和n2分别表示三棱镜对a光和b光的折射率,用v1和v2分别表示a光和b光在三棱镜中的光速,用λ1和λ2分别表示a光和b光在三棱镜中的波长,下列说法正确的是( )
 如图所示,一细束a光和一细束b光平行射到同一个三棱镜上,经折射后交于光屏上的同一个点M,若用n1和n2分别表示三棱镜对a光和b光的折射率,用v1和v2分别表示a光和b光在三棱镜中的光速,用λ1和λ2分别表示a光和b光在三棱镜中的波长,下列说法正确的是( )
如图所示,一细束a光和一细束b光平行射到同一个三棱镜上,经折射后交于光屏上的同一个点M,若用n1和n2分别表示三棱镜对a光和b光的折射率,用v1和v2分别表示a光和b光在三棱镜中的光速,用λ1和λ2分别表示a光和b光在三棱镜中的波长,下列说法正确的是( )| A. | n1>n2,λ1<λ2,v1<v2 | B. | n1<n2,λ1<λ2,v1<v2 | ||
| C. | n1<n2,λ1>λ2,v1<v2 | D. | n1>n2,λ1<λ2,v1>v2 |
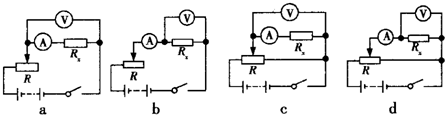
13. 如图所示,一理想变压器原线圈的匝数n1=1100匝,副线圈的匝数n2=220匝,交流电源的电压u=220$\sqrt{2}$sin(100πt)V,电阻R=44Ω,电压表、电流表均为理想电表,下列表述正确的是( )
如图所示,一理想变压器原线圈的匝数n1=1100匝,副线圈的匝数n2=220匝,交流电源的电压u=220$\sqrt{2}$sin(100πt)V,电阻R=44Ω,电压表、电流表均为理想电表,下列表述正确的是( )
 如图所示,一理想变压器原线圈的匝数n1=1100匝,副线圈的匝数n2=220匝,交流电源的电压u=220$\sqrt{2}$sin(100πt)V,电阻R=44Ω,电压表、电流表均为理想电表,下列表述正确的是( )
如图所示,一理想变压器原线圈的匝数n1=1100匝,副线圈的匝数n2=220匝,交流电源的电压u=220$\sqrt{2}$sin(100πt)V,电阻R=44Ω,电压表、电流表均为理想电表,下列表述正确的是( )| A. | 交流电的周期为0.01 s | B. | 电压表的示数为44V | ||
| C. | 电流表A2的示数约为1.4A | D. | 电流表A1的示数为0.2A |

 金属棒bc在两光滑的水平固定放置的平行金属导轨上向右运动,回路中有垂直纸面向里的匀强磁场,这时回路中感应电流的方向为逆时针(填“顺时针”或“逆时针”),bc棒将受到方向向左(填“左”或“右”)的安培力;为使bc棒向右匀速运动,必须对bc棒施加方向向右(填“左”或“右”)的外力.
金属棒bc在两光滑的水平固定放置的平行金属导轨上向右运动,回路中有垂直纸面向里的匀强磁场,这时回路中感应电流的方向为逆时针(填“顺时针”或“逆时针”),bc棒将受到方向向左(填“左”或“右”)的安培力;为使bc棒向右匀速运动,必须对bc棒施加方向向右(填“左”或“右”)的外力.