题目内容
4. 如图所示,斜面轨道AB与水平面之间的夹角θ=53°,BD为半径R=4m的圆弧形轨道,且B点与D点在同一水平面上,在B点,斜面轨道AB与圆弧形轨道BD相切,整个轨道处于竖直平面内且处处光滑,在A点处有一质量m=1kg的小球由静止滑下,经过B、C两点后从D点斜抛出去,最后落在地面上的S点时的速度大小vS=8m/s,已知A点距地面的高度H=10m,B点距地面的高度h=5m,设以MDN为分界线,其左边为一阻力场区域,右边为真空区域,g取10m/s2,cos53°=0.6,求:
如图所示,斜面轨道AB与水平面之间的夹角θ=53°,BD为半径R=4m的圆弧形轨道,且B点与D点在同一水平面上,在B点,斜面轨道AB与圆弧形轨道BD相切,整个轨道处于竖直平面内且处处光滑,在A点处有一质量m=1kg的小球由静止滑下,经过B、C两点后从D点斜抛出去,最后落在地面上的S点时的速度大小vS=8m/s,已知A点距地面的高度H=10m,B点距地面的高度h=5m,设以MDN为分界线,其左边为一阻力场区域,右边为真空区域,g取10m/s2,cos53°=0.6,求:(1)小球经过B点时的速度为多大?
(2)小球经过圆弧轨道最低处C点时对轨道的压力多大?
(3)求小球从D点至S点的过程中阻力f所做的功.
分析 (1)小球从A到B的过程中只有重力做功,根据机械能守恒求解小球经过B点的速度.
(2)根据机械能定律求出小球经过C点时的速度.由牛顿第二定律求出轨道对小球的支持力.
(3)小球从D点至S点的过程中,根据动能定理求解阻力f所做的功.
解答 解:(1)设小球经过B点时的速度大小为vB,对小球从A到B的过程,由机械能守恒得:
$mg(H-h)=\frac{1}{2}mv_B^2$
解得:vB=$\sqrt{2g(H-h)}$=$\sqrt{2×10(10-5)}$m/s=10m/s.
(2)设小球经过C点时的速度为vC,由机械能守恒得:$mgR(1-cos{53^0})+\frac{1}{2}mv_B^2=\frac{1}{2}mv_C^2$
轨道对小球的支持力N,根据牛顿第二定律可得:N-mg=$m\frac{v_C^2}{R}$
由以上两式得,N=1.8mg+$m\frac{{v}_{B}^{2}}{R}$=1.8×1×10N+$1×\frac{1{0}^{2}}{4}N$=43N.
则小球对轨道的压力为N′=N=43N,则
(3)设小球受到的阻力为f,到达S点的速度为vS,在此过程中阻力所做的功为W,易知vD=vB,
由动能定理可得:$mgh+W=\frac{1}{2}mv_S^2-\frac{1}{2}mv_D^2$
代入解得W=-68J
答:
(1)小球经过B点的速度为10m/s.
(2)小球经过圆弧轨道最低处C点时对轨道的压力43N.
(3)小球从D点至S点的过程中,阻力f所做的功为-68J.
点评 本题是机械能守恒定律、牛顿第二定律、动能定理的综合应用,常见的陈题.小球从D点抛出后,阻力是变力,不能根据功的计算公式求阻力做功,运用动能定理求变力做功是常用的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6. 如图甲所示,质量不计的弹簧竖直固定在水平地面上,t=0时刻,将一金属小球从弹簧正上方某一高度处由静止释放,小球落到弹簧上压缩弹簧到最低点,然后又被弹簧弹起离开弹簧,上升到一定高度后再下落,如此反复.通过安装在弹簧下端的压力传感器,测出这一过程弹簧弹力F随时间t变化的图象如图乙所示,则( )
如图甲所示,质量不计的弹簧竖直固定在水平地面上,t=0时刻,将一金属小球从弹簧正上方某一高度处由静止释放,小球落到弹簧上压缩弹簧到最低点,然后又被弹簧弹起离开弹簧,上升到一定高度后再下落,如此反复.通过安装在弹簧下端的压力传感器,测出这一过程弹簧弹力F随时间t变化的图象如图乙所示,则( )
 如图甲所示,质量不计的弹簧竖直固定在水平地面上,t=0时刻,将一金属小球从弹簧正上方某一高度处由静止释放,小球落到弹簧上压缩弹簧到最低点,然后又被弹簧弹起离开弹簧,上升到一定高度后再下落,如此反复.通过安装在弹簧下端的压力传感器,测出这一过程弹簧弹力F随时间t变化的图象如图乙所示,则( )
如图甲所示,质量不计的弹簧竖直固定在水平地面上,t=0时刻,将一金属小球从弹簧正上方某一高度处由静止释放,小球落到弹簧上压缩弹簧到最低点,然后又被弹簧弹起离开弹簧,上升到一定高度后再下落,如此反复.通过安装在弹簧下端的压力传感器,测出这一过程弹簧弹力F随时间t变化的图象如图乙所示,则( )| A. | t2时刻弹簧的弹性势能最大 | |
| B. | t3时刻弹簧的弹性势能最大 | |
| C. | t1~t3这段时间内,弹簧的弹性势能先减小后增加 | |
| D. | t1~t3这段时间内,弹簧的弹性势能先增加后减少 |
19.一个质点受5个力的作用而静止,当撤去一个向东10N的力和一个向北偏西30°、20N的力以后,质点失去平衡.为了使质点恢复平衡,再给质点加一个力,这个力的大小和方向是( )
| A. | 10$\sqrt{3}$N,向北 | B. | 10$\sqrt{3}$N,向南 | C. | 10$\sqrt{5}$N,北偏东30° | D. | 10$\sqrt{5}$N,南偏西30° |
9. 如图所示,沿x轴正方向传播的一列横波在某时刻的波形图为一正弦曲线,其波速为200m/s,下列说法中正确的是( )
如图所示,沿x轴正方向传播的一列横波在某时刻的波形图为一正弦曲线,其波速为200m/s,下列说法中正确的是( )
 如图所示,沿x轴正方向传播的一列横波在某时刻的波形图为一正弦曲线,其波速为200m/s,下列说法中正确的是( )
如图所示,沿x轴正方向传播的一列横波在某时刻的波形图为一正弦曲线,其波速为200m/s,下列说法中正确的是( )| A. | 从图示时刻开始,经过0.01 s质点a通过的路程为0.4 m | |
| B. | 从图示时刻开始,质点b比质点a先到平衡位置 | |
| C. | 平衡位置为x=2的质点与平衡位置为x=4的质点反相 | |
| D. | 图示时刻质点b的加速度方向向下 |
16. 如图所示,轻质光滑滑轮两侧用细绳连着两个物体A与B,物体B放在水平地面上,A、B均静止.已知A和B的质量分别为m、M,绳与水平方向的夹角为θ,则( )
如图所示,轻质光滑滑轮两侧用细绳连着两个物体A与B,物体B放在水平地面上,A、B均静止.已知A和B的质量分别为m、M,绳与水平方向的夹角为θ,则( )
 如图所示,轻质光滑滑轮两侧用细绳连着两个物体A与B,物体B放在水平地面上,A、B均静止.已知A和B的质量分别为m、M,绳与水平方向的夹角为θ,则( )
如图所示,轻质光滑滑轮两侧用细绳连着两个物体A与B,物体B放在水平地面上,A、B均静止.已知A和B的质量分别为m、M,绳与水平方向的夹角为θ,则( )| A. | 物体B受到的摩擦力可能为0 | B. | 物体B受到的摩擦力为mgcosθ | ||
| C. | 物体B对地面的压力可能为0 | D. | 物体B对地面的压力为Mg-mgsinθ |
14. 如图所示,电路中理想变压器原、副线圈接入电路的匝数可通过单刀双掷开关改变,A为交流电流表.在变压器原线圈a、b两端加上一峰值不变的正弦交变电压.下列分析正确的是( )
如图所示,电路中理想变压器原、副线圈接入电路的匝数可通过单刀双掷开关改变,A为交流电流表.在变压器原线圈a、b两端加上一峰值不变的正弦交变电压.下列分析正确的是( )
 如图所示,电路中理想变压器原、副线圈接入电路的匝数可通过单刀双掷开关改变,A为交流电流表.在变压器原线圈a、b两端加上一峰值不变的正弦交变电压.下列分析正确的是( )
如图所示,电路中理想变压器原、副线圈接入电路的匝数可通过单刀双掷开关改变,A为交流电流表.在变压器原线圈a、b两端加上一峰值不变的正弦交变电压.下列分析正确的是( )| A. | 只将S1从1拨向2时,电流表示数变小 | |
| B. | 只将S2从3拨向4时,电流表示数变大 | |
| C. | 只将R的滑片上移,R2的电功率变大 | |
| D. | 只将R的滑片上移,变压器的输入功率减小 |
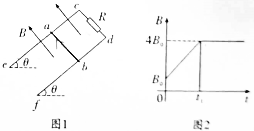 如图1所示,由足够长的平行金属轨道ce、df确定的平面与水平面间的夹角为θ=60°,c、d端接有阻值为R的电阻,导体棒ab垂直于轨道放置在轨道上.轨道间距离为L,轨道间垂直于轨道平面向上的匀强磁场,磁感应强度B随时间t的变化规律如图2所示.0-t1时间内,棒ab静止在轨道上,且t1时刻恰好要沿轨道滑动,棒ab与cd端的距离为L.棒ab与两轨道接触良好,且其沿轨道下滑过程中始终与轨道垂直,轨道和棒的电阻不计,最大静摩擦力等于滑动摩擦力,求:
如图1所示,由足够长的平行金属轨道ce、df确定的平面与水平面间的夹角为θ=60°,c、d端接有阻值为R的电阻,导体棒ab垂直于轨道放置在轨道上.轨道间距离为L,轨道间垂直于轨道平面向上的匀强磁场,磁感应强度B随时间t的变化规律如图2所示.0-t1时间内,棒ab静止在轨道上,且t1时刻恰好要沿轨道滑动,棒ab与cd端的距离为L.棒ab与两轨道接触良好,且其沿轨道下滑过程中始终与轨道垂直,轨道和棒的电阻不计,最大静摩擦力等于滑动摩擦力,求: 实验课上老师布置了两项任务:①测量一个电流计的内电阻,②测量干电池的电动势与内电阻,实验台上准备了如下器材:
实验课上老师布置了两项任务:①测量一个电流计的内电阻,②测量干电池的电动势与内电阻,实验台上准备了如下器材: 如图所示,A、B质量分别为ml=1kg,m2=2kg,置于小车C上,小车质量m3=1kg,A、B间粘有少量炸药,A、B与小车间的动摩擦因数均为0.5,小车静止在光滑水平上,炸药爆炸释放的能量有12J转化为A、B的机械能,其余的转化为内能,A、B始终在小车表面水平运动,求:
如图所示,A、B质量分别为ml=1kg,m2=2kg,置于小车C上,小车质量m3=1kg,A、B间粘有少量炸药,A、B与小车间的动摩擦因数均为0.5,小车静止在光滑水平上,炸药爆炸释放的能量有12J转化为A、B的机械能,其余的转化为内能,A、B始终在小车表面水平运动,求: