题目内容
10. 如图所示,两个质量都是m的滑块A和B,紧挨着并排放在水平桌面上,A、B间的接触面垂直于图中纸面且与水平面成θ角,所有接触面都光滑无摩擦,现用一个水平推力作用于滑块A上,使A、B一起向右做加速运动,试求:
如图所示,两个质量都是m的滑块A和B,紧挨着并排放在水平桌面上,A、B间的接触面垂直于图中纸面且与水平面成θ角,所有接触面都光滑无摩擦,现用一个水平推力作用于滑块A上,使A、B一起向右做加速运动,试求:(1)如果要A、B间不发生相对滑动,它们共同向右的最大加速度是多少?
(2)要使A、B间不发生相对滑动,水平推力的大小应在什么范围内才行?
分析 当地面对A的支持力为零时,推力F最大,此时两个物体的加速度仍相同,由牛顿第二定律与平衡条件可以求出最大的推力.对整体研究,根据牛顿第二定律求出最大加速度.
解答 解:设A、B间的弹力为N,地面对B的支持力为N′,推力F越大,则A越可能相对于B向上滑,当F最大时,A刚要相对B向上滑,A不受地面的支持力,设A、B共同以加速度a沿地面加速前进.
对A有:F-N sinθ=ma,N cosθ=mg
对B有:Nsinθ=ma
解得最大推力:Fmax=2mgtanθ.
则向右的最大加速度${a}_{m}=\frac{{F}_{max}}{2m}=gtanθ$.
答:(1)如果要A、B间不发生相对滑动,它们共同向右的最大加速度是gtanθ;
(2)水平推力的范围为0<F≤2mgtanθ.
点评 解题的关键是知道两物体刚好不发生相对滑动的临界条件:地面对A的支持力为零,应用牛顿第二定律即可正确解题,解题时要注意研究对象的选择.

练习册系列答案
相关题目
20. 氢原子的能级图如图所示,一群处于n=3激发态的氢原子向基态跃迁,发出波长不同的三种光子,设它们在真空中的波长分别为λ1、λ2、λ3,且λ1<λ2<λ3,则下列说法中正确的是( )
氢原子的能级图如图所示,一群处于n=3激发态的氢原子向基态跃迁,发出波长不同的三种光子,设它们在真空中的波长分别为λ1、λ2、λ3,且λ1<λ2<λ3,则下列说法中正确的是( )
 氢原子的能级图如图所示,一群处于n=3激发态的氢原子向基态跃迁,发出波长不同的三种光子,设它们在真空中的波长分别为λ1、λ2、λ3,且λ1<λ2<λ3,则下列说法中正确的是( )
氢原子的能级图如图所示,一群处于n=3激发态的氢原子向基态跃迁,发出波长不同的三种光子,设它们在真空中的波长分别为λ1、λ2、λ3,且λ1<λ2<λ3,则下列说法中正确的是( )| A. | 波长为λ1的光在玻璃砖内的传播速度最大 | |
| B. | λ1、λ2、λ3之间的关系为λ1=$\frac{{{λ_2}{λ_3}}}{{{λ_2}+{λ_3}}}$ | |
| C. | 用该三种光做双缝干涉实验时,同样条件下用波长为λ1的光得到的条纹间距最大 | |
| D. | 让波长为λ2的光子照射逸出功为2.7eV的钙,则释放出的光子的最大初动能为7.5ev |
1. 如图所示,竖直绝缘墙壁上有一固定的质点A,在A的正上方的P点用丝线悬挂另一质点B,A、B两质点因为带电而相互排斥,致使悬线与竖直方向成θ角,由于漏电使A、B两质点的电荷量逐渐减少,在电荷漏电完毕之前悬线对悬点P的拉力大小( )
如图所示,竖直绝缘墙壁上有一固定的质点A,在A的正上方的P点用丝线悬挂另一质点B,A、B两质点因为带电而相互排斥,致使悬线与竖直方向成θ角,由于漏电使A、B两质点的电荷量逐渐减少,在电荷漏电完毕之前悬线对悬点P的拉力大小( )
 如图所示,竖直绝缘墙壁上有一固定的质点A,在A的正上方的P点用丝线悬挂另一质点B,A、B两质点因为带电而相互排斥,致使悬线与竖直方向成θ角,由于漏电使A、B两质点的电荷量逐渐减少,在电荷漏电完毕之前悬线对悬点P的拉力大小( )
如图所示,竖直绝缘墙壁上有一固定的质点A,在A的正上方的P点用丝线悬挂另一质点B,A、B两质点因为带电而相互排斥,致使悬线与竖直方向成θ角,由于漏电使A、B两质点的电荷量逐渐减少,在电荷漏电完毕之前悬线对悬点P的拉力大小( )| A. | 变小 | B. | 变大 | C. | 不变 | D. | 无法确定 |
2. 如图所示,带电金属小球用绝缘丝线系住,丝线上端固定,形成一个摆,如果在摆球经过的区域加上如图所示的磁场,不计摩擦及空气阻力,下列说法中不正确的是( )
如图所示,带电金属小球用绝缘丝线系住,丝线上端固定,形成一个摆,如果在摆球经过的区域加上如图所示的磁场,不计摩擦及空气阻力,下列说法中不正确的是( )
 如图所示,带电金属小球用绝缘丝线系住,丝线上端固定,形成一个摆,如果在摆球经过的区域加上如图所示的磁场,不计摩擦及空气阻力,下列说法中不正确的是( )
如图所示,带电金属小球用绝缘丝线系住,丝线上端固定,形成一个摆,如果在摆球经过的区域加上如图所示的磁场,不计摩擦及空气阻力,下列说法中不正确的是( )| A. | 摆球每次通过最低点时丝线拉力大小不相等 | |
| B. | 摆球每次通过最低点时动能相等 | |
| C. | 摆球每次离开最低点时的最大距离逐渐减少 | |
| D. | 摆球每次在上丝线最大偏角处丝线的拉力大小不变 |
19. 用两辆拖拉机拉一辆陷入泥坑的卡车,如图所示,一辆拖拉机沿与卡车前进方向成45°角、用大小为1000$\sqrt{2}$N的力F1拉卡车,另一辆拖拉机沿与卡车前进方向成30°、用大小为2×103N的力F2拉卡车,卡车开动后自身向前提供的动力为4×103N,三车同时作用,刚好使卡车脱离泥坑,则卡车受到的阻力约为( )
用两辆拖拉机拉一辆陷入泥坑的卡车,如图所示,一辆拖拉机沿与卡车前进方向成45°角、用大小为1000$\sqrt{2}$N的力F1拉卡车,另一辆拖拉机沿与卡车前进方向成30°、用大小为2×103N的力F2拉卡车,卡车开动后自身向前提供的动力为4×103N,三车同时作用,刚好使卡车脱离泥坑,则卡车受到的阻力约为( )
 用两辆拖拉机拉一辆陷入泥坑的卡车,如图所示,一辆拖拉机沿与卡车前进方向成45°角、用大小为1000$\sqrt{2}$N的力F1拉卡车,另一辆拖拉机沿与卡车前进方向成30°、用大小为2×103N的力F2拉卡车,卡车开动后自身向前提供的动力为4×103N,三车同时作用,刚好使卡车脱离泥坑,则卡车受到的阻力约为( )
用两辆拖拉机拉一辆陷入泥坑的卡车,如图所示,一辆拖拉机沿与卡车前进方向成45°角、用大小为1000$\sqrt{2}$N的力F1拉卡车,另一辆拖拉机沿与卡车前进方向成30°、用大小为2×103N的力F2拉卡车,卡车开动后自身向前提供的动力为4×103N,三车同时作用,刚好使卡车脱离泥坑,则卡车受到的阻力约为( )| A. | 8.2×103 N | B. | 6.0×103 N | C. | 5.6×103 N | D. | 6.7×103 N |
20.关于多普勒效应,下列说法正确的是( )
| A. | 多普勒效应是由波的干涉引起的 | |
| B. | 多普勒效应是由于波源和观察者之间有相对运动而产生的 | |
| C. | 多普勒效应不能说明波源的频率发生了变化 | |
| D. | 声波可以产生多普勒效应 |

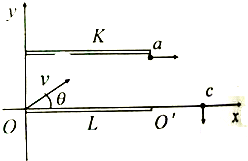 如图所示,有一平行板电容器左边缘在y轴上,下极板与x轴重合,极板间匀强电场的场强为E,一电量为q,质量为m的带电粒子,速度大小为$\sqrt{3}$$\frac{E}{B}$,从O点与x轴成θ角斜向上射入极板间,粒子经过K板边缘a点平行于x轴飞出电容器,立即进入一磁感应强度为B的圆形磁场(图中未画),随后从c点垂直穿过x轴离开磁场.已知∠acO=45°,cosθ=$\frac{\sqrt{3}}{3}$,磁场方向垂直于坐标平面向外,带电粒子重力不计,试求:
如图所示,有一平行板电容器左边缘在y轴上,下极板与x轴重合,极板间匀强电场的场强为E,一电量为q,质量为m的带电粒子,速度大小为$\sqrt{3}$$\frac{E}{B}$,从O点与x轴成θ角斜向上射入极板间,粒子经过K板边缘a点平行于x轴飞出电容器,立即进入一磁感应强度为B的圆形磁场(图中未画),随后从c点垂直穿过x轴离开磁场.已知∠acO=45°,cosθ=$\frac{\sqrt{3}}{3}$,磁场方向垂直于坐标平面向外,带电粒子重力不计,试求: 有一种“傻瓜”照相机,其光圆(进光孔径)随被拍摄物体的高度自动调节,而快门(曝光时间)是固定不变的,实验者从某砖墙的高处使一个石子自由落下,拍摄石子在空中的照片如图所示,由于石子的运动,它在照片上留下了一条模糊的径迹,已知该照相机的曝光时间为0.02s,每块砖的平均厚度为6cm,试估算拍摄到的石子从距位置A多高处开始下落的?
有一种“傻瓜”照相机,其光圆(进光孔径)随被拍摄物体的高度自动调节,而快门(曝光时间)是固定不变的,实验者从某砖墙的高处使一个石子自由落下,拍摄石子在空中的照片如图所示,由于石子的运动,它在照片上留下了一条模糊的径迹,已知该照相机的曝光时间为0.02s,每块砖的平均厚度为6cm,试估算拍摄到的石子从距位置A多高处开始下落的?