题目内容
如图所示，一个可视为质点的物块，质量为m=2 kg，从光滑四分之一圆弧轨道顶端由静止滑下，到达底端时恰好进入与圆弧轨道底端相切的水平传送带，传送带由一电动机驱动着匀速向左转动，速度大小为u=3 m/s。已知圆弧轨道半径R=0.8 m，皮带轮的半径r=0.2m，物块与传送带间的动摩擦因数为μ=0.1，两皮带轮之间的距离为L=6m，重力加速度g=10m/s2。求：
（1）皮带轮转动的角速度多大？
（2）物块滑到圆弧轨道底端时对轨道的作用力；
（3）物块将从传送带的哪一端离开传送带？物块在传送带上克服摩擦力所做的功为多大？
【答案】
（1）15rad/s（2）60N，方向竖直向下。（3）12J
【解析】弄清楚物体的运动过程和受力情况是解题关键。①物块沿光滑圆弧下滑的过程，机械能守恒；②物块在传送带上做匀减速直线运动。
（1）皮带轮转动的角速度，由u=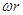
，得
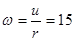rad/s （2分）
（2）物块滑到圆弧轨道底端的过程中，由动能定理得
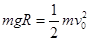（1分）
解得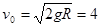
m/s （1分）
在圆弧轨道底端，由牛顿第二定律得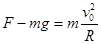 
（2分）
解得物块所受支持力 F=60N （1分）
由牛顿第三定律，物块对轨道的作用力大小为60N，方向竖直向下。 （1分）
（3）物块滑上传送带后做匀减速直线运动，设加速度大小为a，由牛顿第二定律得
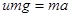（1分）
解得 a=1m/s2 （1分）
物块匀减速到速度为零时运动的最大距离为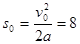 
m
> L=6m （1分）
可见，物块将从传送带的右端离开传送带。 （1分）
物块在传送带上克服摩擦力所做的功为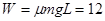
J。
（2分）
误区警示：计算物块在传送带上运动时的位移以及摩擦力做功时，不少学生容易受到传送带运动的影响而出错。
练习册系列答案
相关题目
如图所示，一个可视为质点的物块，质量为m=2kg，从光滑四分之一圆弧轨道顶端由静止滑下，到达底端时恰好进入与圆弧轨道底端相切的水平传送带，传送带由一电动机驱动着匀速向左转动，速度大小为u=3m/s．已知圆弧轨道半径R=0.8m，皮带轮的半径r=0.2m，物块与传送带间的动摩擦因数为μ=0.1，两皮带轮之间的距离为L=6m，重力加速度g=10m/s2．求：
如图所示，一个可视为质点的质量为m的小球以初速度v飞出高为H的桌面，当它经过距离地面高为h的A点时，所具有的机械能是（以桌面为零势能面，不计空气阻力）（ ）
如图所示，一个可视为质点的物块，质量为m=2kg，从光滑四分之一圆弧轨道顶端由静止滑下，到达底端时恰好进入与圆弧轨道底端相切的水平传送带，传送带由一电动机驱动着匀速向左转动，R=0.8m速度大小为v=3m/s．物块与传送带间的动摩擦因数为．μ=0.1，两皮带轮之间的距离为L=6m，重力加速度g=1Om/s2．求：