题目内容
8. 如图所示,一滑块从倾角为370的斜面顶端由静止下滑,滑到底端后又在水平面上滑行一段距离静止,已知斜面高为0.6m,滑块与斜面和水平面的动摩擦因数均为0.5,求滑块在水平面滑行的距离.(本题要求分别用牛顿定律和动能定理两种方法求解,每种方法7分)
如图所示,一滑块从倾角为370的斜面顶端由静止下滑,滑到底端后又在水平面上滑行一段距离静止,已知斜面高为0.6m,滑块与斜面和水平面的动摩擦因数均为0.5,求滑块在水平面滑行的距离.(本题要求分别用牛顿定律和动能定理两种方法求解,每种方法7分)
分析 方法一:根据牛顿第二定律分别求出物体在斜面和水平面上运动的加速度,再结合运动学公式,即可求解
方法二:以滑块开始运动到停止在平面上全过程为研究过程,由动能定理可以求出物体在水平面上滑行的距离.
解答 解:方法一:牛顿定律
设滑块在斜面上的加速度大小为a1
根据牛顿定律:mgsinθ-μmgcosθ=ma1
解得:a1=2m/s2
vB2=2a1x1 ①
设滑块在水平面运动的加速度大小为a2
根据牛顿定律:μmg=ma2
解得:a2=5m/s2
vB2=2a2x2 ②
解①②联立方程组得x2=0.4m
方法二:动能定理
以滑块开始运动到停止在平面上全过程为研究过程
mgh-μmgcosθx1-μmgx2=0
X1=$\frac{h}{sinθ}$
解得:X2=0.4m
答:滑块在水平面滑行的距离为0.4m
点评 本题通过动能定理解决比较简便,由牛顿第二定律和运动学公式结合求解时,求解加速度是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5. 图示矩形线圈在匀强磁场中匀速转动,产生的感应电动势最大值为50V,那么该线圈从图示位置转过60°时,感应电动势的瞬时值大小为( )
图示矩形线圈在匀强磁场中匀速转动,产生的感应电动势最大值为50V,那么该线圈从图示位置转过60°时,感应电动势的瞬时值大小为( )
 图示矩形线圈在匀强磁场中匀速转动,产生的感应电动势最大值为50V,那么该线圈从图示位置转过60°时,感应电动势的瞬时值大小为( )
图示矩形线圈在匀强磁场中匀速转动,产生的感应电动势最大值为50V,那么该线圈从图示位置转过60°时,感应电动势的瞬时值大小为( )| A. | 50V | B. | 25$\sqrt{3}$V | C. | 25$\sqrt{2}$ | D. | 25V |
3.完全相同的两辆汽车,都拖着完全相同的拖车(与汽车质量相等)以相同的速度在平直公路上以速度v匀速齐头并迸,汽车与拖车的质量均为m,某一时刻两拖车同时与汽车脱离之后,甲汽车保持原来的牵引力继续前进,乙汽车保持原来的功率继续前进,经过一段时间后甲车的速度变为2v,乙车的速度变为1.5v,若路面对汽车的阻力恒为车重的0.1倍,取g=10m/s2,则此时( )
| A. | 甲乙两车在这段时间内牵引力做功之比为3:2 | |
| B. | 甲乙两车在这段时间内的位移之比为4:3 | |
| C. | 甲乙两车在这段时间内克服阻力做功之比为12:11 | |
| D. | 甲车的功率增大到原来的4倍 |
13. 如图所示,木块A放在木板B的左上端,用恒力F将A拉至B的右端,第1次将B固定在地面上,木块A获得的动能为Ek;第2次可以让B在光滑的地面上自由的滑动,木块A获得的动能为Ek′.比较两次木块A获得的动能,则( )
如图所示,木块A放在木板B的左上端,用恒力F将A拉至B的右端,第1次将B固定在地面上,木块A获得的动能为Ek;第2次可以让B在光滑的地面上自由的滑动,木块A获得的动能为Ek′.比较两次木块A获得的动能,则( )
 如图所示,木块A放在木板B的左上端,用恒力F将A拉至B的右端,第1次将B固定在地面上,木块A获得的动能为Ek;第2次可以让B在光滑的地面上自由的滑动,木块A获得的动能为Ek′.比较两次木块A获得的动能,则( )
如图所示,木块A放在木板B的左上端,用恒力F将A拉至B的右端,第1次将B固定在地面上,木块A获得的动能为Ek;第2次可以让B在光滑的地面上自由的滑动,木块A获得的动能为Ek′.比较两次木块A获得的动能,则( )| A. | Ek<Ek′ | B. | Ek=Ek′ | C. | Ek>Ek′ | D. | 无法确定 |
20.雾霾天气是对大气中各种悬浮颗粒物含量超标的笼统表述,是特定气候条件与人类活动相互作用的结果.雾霾中,各种悬浮颗粒物形状不规则,但可视为密度相同、直径不同的球体,并用PM10、PM2.5分别表示直径小于或等于10μm、2.5μm的颗粒物(PM是颗粒物的英文缩写).某科研机构对北京地区的检测结果表明,在静稳的雾霾天气中,近地面高度百米的范围内,PM10的浓度随高度的增加略有减小,大于PM10的大悬浮颗粒物的浓度随高度的增加明显减小,且两种浓度分布基本不随时间变化.据此材料,以下叙述正确的是( )
| A. | PM10表示直径小于或等于1.0×10-6 m的悬浮颗粒物 | |
| B. | PM10受到的空气分子作用力的合力始终等于其受到的重力 | |
| C. | PM2.5浓度随高度的增加逐渐增大 | |
| D. | PM10和大悬浮颗粒物都在做布朗运动 |
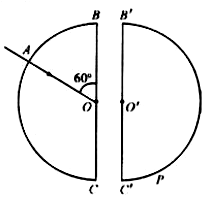 如图所示,两块半径均为R的半圆形玻璃砖平行对称放置,沿竖直方向的两条直径BC、B′C′相互平行,两圆心之间的距离为$\frac{R}{3}$.一束单色光正对圆心O从A点射入左侧的玻璃砖,最后从右侧玻璃砖上的P点射出.已知∠AOB=60°,玻璃折射率为n=$\sqrt{3}$,若不考虑光在各个界面的反射.
如图所示,两块半径均为R的半圆形玻璃砖平行对称放置,沿竖直方向的两条直径BC、B′C′相互平行,两圆心之间的距离为$\frac{R}{3}$.一束单色光正对圆心O从A点射入左侧的玻璃砖,最后从右侧玻璃砖上的P点射出.已知∠AOB=60°,玻璃折射率为n=$\sqrt{3}$,若不考虑光在各个界面的反射. 如图所示,物体在离斜面底端L处由静止开始下滑,然后滑上由小圆弧(长度忽略)与斜面连接的水平面上,水平面足够长,动摩擦因数为0.5.若斜面是光滑的,物体在水平面上滑行的距离为s1;若斜面粗糙,动摩擦因数也为0.5,物体在水平面上滑行的距离为s2.斜面倾角为37°,求s1:s2为多少?(已知sin37°=0.6,cos37°=0.8)
如图所示,物体在离斜面底端L处由静止开始下滑,然后滑上由小圆弧(长度忽略)与斜面连接的水平面上,水平面足够长,动摩擦因数为0.5.若斜面是光滑的,物体在水平面上滑行的距离为s1;若斜面粗糙,动摩擦因数也为0.5,物体在水平面上滑行的距离为s2.斜面倾角为37°,求s1:s2为多少?(已知sin37°=0.6,cos37°=0.8) 在光滑的水平地面上有质量为M的长木板A(如图所示),长木板上放一质量为m的物体B,A、B之间动摩擦因数为μ.今在物体B上加一水平恒力F,B和A发生相对滑动,经过时间t,求
在光滑的水平地面上有质量为M的长木板A(如图所示),长木板上放一质量为m的物体B,A、B之间动摩擦因数为μ.今在物体B上加一水平恒力F,B和A发生相对滑动,经过时间t,求