题目内容
14. 如图所示,第一、四象限内存在一匀强电场,其方向如图所示.第二象限内有垂直纸面向外磁感应强度为B的匀强磁场,一个质量为m,电荷量为+q(不计重力) 的带电粒子从x轴上的A点以初速度v0沿垂直于磁感线方向进入匀强磁场中,初速度方向与x轴负方向的夹角θ=30°粒子恰好从 y轴上的P点垂直于电场线的方向射入匀强电场,经过x轴上的C点再到达 y轴上的D点,已知AO=OC(P、D两点图中未标出 ),
如图所示,第一、四象限内存在一匀强电场,其方向如图所示.第二象限内有垂直纸面向外磁感应强度为B的匀强磁场,一个质量为m,电荷量为+q(不计重力) 的带电粒子从x轴上的A点以初速度v0沿垂直于磁感线方向进入匀强磁场中,初速度方向与x轴负方向的夹角θ=30°粒子恰好从 y轴上的P点垂直于电场线的方向射入匀强电场,经过x轴上的C点再到达 y轴上的D点,已知AO=OC(P、D两点图中未标出 ),求:
(1)匀强电场的电场强度E的大小;
(2)粒子到达D点的速度大小及从A运动到D所用的时间.
分析 (l)粒子在磁场中做的是匀速圆周运动,由洛伦兹力提供向心力,由牛顿第二定律求出轨迹半径.粒子进入电场后做类平抛运动,在竖直方向上做的是匀加速直线运动,根据粒子匀加速运动的位移可以求得匀强电场的场强的大小;
(2)根据平行于电场线和垂直于电场线两个方向的分位移公式,求出分位移,得到时间,由动能定理求粒子到达D点的速度大小.
在磁场中,根据粒子的运动的轨迹可以求得粒子的运动的时间,即可得到总时间.
解答  解:(1)设粒子在磁场中圆周运动的半径为R.
解:(1)设粒子在磁场中圆周运动的半径为R.
由牛顿第二定律得 qv0B=m$\frac{{v}_{0}^{2}}{R}$,则 R=$\frac{m{v}_{0}}{qB}$
在电场中,粒子做类平抛运动,沿电场线方向有分位移:y=R=$\frac{1}{2}a{t}^{2}$
根据牛顿第二定律得 a=$\frac{qE}{m}$
平行于电场线方向有 x=2Rcos30°=v0t;
由以上各式联立得 E=$\frac{2B{v}_{0}}{3}$.
(2)平行于电场线方向的位移 y=$\frac{1}{2}a{t}_{2}^{2}$
垂直于电场线方向的位移 x=ytan30°=v0t2;
联立得 y=$\frac{9m{v}_{0}}{qB}$,t2=$\frac{3\sqrt{3}m}{qB}$
由动能定理得
qEy=$\frac{1}{2}m{v}^{2}-\frac{1}{2}m{v}_{0}^{2}$
解得 v=$\sqrt{13}{v}_{0}$
故从A运动到D所用的时间为 t=$\frac{1}{2}T$+t2=$\frac{πm}{qB}$+$\frac{3\sqrt{3}m}{qB}$=$\frac{m}{qB}$($π+3\sqrt{3}$)
答:
(1)匀强电场的电场强度E的大小为$\frac{2B{v}_{0}}{3}$;
(2)粒子到达D点的速度大小为$\sqrt{13}{v}_{0}$,从A运动到D所用的时间为$\frac{m}{qB}$($π+3\sqrt{3}$).
点评 粒子先做的是匀速圆周运动,后在电场中做类平抛运动,根据匀速圆周运动和类平抛运动的规律可以分别求得.

 如图所示,竖直放置的两块很大的平行金属板a、b,相距为d,ab间的电场强度为E,今有一带正电的微粒从a板下缘以初速度v0竖直向上射入电场,当它飞到b板时,速度大小不变,而方向变为水平方向,且刚好从高度也为d的狭缝穿过b板而进入bc区域,bc区域的宽度也为d,所加电场大小为E,其方向竖直向上,磁场的磁感应强度大小等于$\frac{E}{{v}_{0}}$,其方向垂直纸面向里,重力加速度为g,则下列关于粒子运动的有关说法正确的是( )
如图所示,竖直放置的两块很大的平行金属板a、b,相距为d,ab间的电场强度为E,今有一带正电的微粒从a板下缘以初速度v0竖直向上射入电场,当它飞到b板时,速度大小不变,而方向变为水平方向,且刚好从高度也为d的狭缝穿过b板而进入bc区域,bc区域的宽度也为d,所加电场大小为E,其方向竖直向上,磁场的磁感应强度大小等于$\frac{E}{{v}_{0}}$,其方向垂直纸面向里,重力加速度为g,则下列关于粒子运动的有关说法正确的是( )| A. | 粒子在ab区域中做匀变速曲线运动 | |
| B. | 粒子在ab区域的运动时间为$\frac{{v}_{0}}{g}$ | |
| C. | 粒子在bc区域中做匀速圆周运动,圆周半径r=d | |
| D. | 粒子在bc区域中做匀速圆周运动,运动时间为$\frac{πd}{6{v}_{0}}$ |
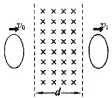 如图所示,宽度为d的有界匀强磁场竖直向下穿过光滑的水平桌面,一质量为m的椭圆形导体框平放在桌面上,椭圆的长轴平行磁场边界,短轴小于d.现给导体框一个初速度v0(v0垂直磁场边界),已知导体框全部在磁场中的速度为v,导体框全部出磁场后的速度为v1:导体框进入磁场过程中产生的焦耳热为Ql 导体框离开磁场过程中产生的焦耳热为Q2,下列说法正确的是( )
如图所示,宽度为d的有界匀强磁场竖直向下穿过光滑的水平桌面,一质量为m的椭圆形导体框平放在桌面上,椭圆的长轴平行磁场边界,短轴小于d.现给导体框一个初速度v0(v0垂直磁场边界),已知导体框全部在磁场中的速度为v,导体框全部出磁场后的速度为v1:导体框进入磁场过程中产生的焦耳热为Ql 导体框离开磁场过程中产生的焦耳热为Q2,下列说法正确的是( )| A. | 导体框离开磁场过程中,读者看到的感应电流的方向为顺时针方向 | |
| B. | 导体框进出磁场都是做匀变速直线运动 | |
| C. | Q1=Q2 | |
| D. | Q1+Q2=$\frac{1}{2}$m(v02-v12) |
| A. | 原子核的结合能等于使其完全分解成自由核子所需的最小能量 | |
| B. | 一重原子核衰变成α粒子和另一原子核,衰变产物的质量之和一定小于原来重核的质量 | |
| C. | 核电站的核能来源于聚变反应 | |
| D. | 比结合能越大,原子核越稳定 | |
| E. | 自由核子组成原子核时,其质量亏损所对应的能量大于该原子核的结合能 |
 如图表示一定质量的理想气体状态变化过程中的四个状态,图中ad平行于横坐标轴,ab的延长线过原点,以下说法正确的是( )
如图表示一定质量的理想气体状态变化过程中的四个状态,图中ad平行于横坐标轴,ab的延长线过原点,以下说法正确的是( )| A. | 从状态d到c,气体不对外做功,外界也不对气体做功 | |
| B. | 从状态c到b,气体对外做负功 | |
| C. | 从状态a到d,气体对外做功 | |
| D. | 从状态b到a,气体不对外做功,内能增加 |
| A. | 布朗发现悬浮在水中的花粉颗粒做无规则运动 | |
| B. | 焦耳通过实验证实,在改变内能的方式上做功和热传递是等效的 | |
| C. | 许多科学家在研究热现象时发现,功转变为热这一现象是可逆的 | |
| D. | 开尔文指出绝对零度是温度的下限,可以达到 | |
| E. | 克劳修斯在大量研究的基础上提出,热量不能自发地从低温物体传到高温物体 |


 用图示装置测量重锤的质量,在定滑轮两侧分别挂上重锤和n块质量均为m0的铁片,重锤下端贴一遮光片,铁架台上安装有光电门.调整重锤的高度,使其从适当的位置由静止开始下落,读出遮光片通过光电门的挡光时间t0;从定滑轮左侧依次取下1块铁片放到右侧重锤上,让重锤每次都从同一位置由静止开始下落,计时器记录的挡光时间分别为t1、t2…,计算出t02、t12….
用图示装置测量重锤的质量,在定滑轮两侧分别挂上重锤和n块质量均为m0的铁片,重锤下端贴一遮光片,铁架台上安装有光电门.调整重锤的高度,使其从适当的位置由静止开始下落,读出遮光片通过光电门的挡光时间t0;从定滑轮左侧依次取下1块铁片放到右侧重锤上,让重锤每次都从同一位置由静止开始下落,计时器记录的挡光时间分别为t1、t2…,计算出t02、t12….