题目内容
如图所示,竖直平平面内有一边长为L、质量为m,电阻为R的正方形线框在竖直向下的匀强重力场和水平方向的磁场组成的复合场以初速度v水平抛出.磁场方向与线框平面垂直,磁场的磁感应强度随竖直向下的z轴按B=B+kz的规律均匀增大.已知重力加速度为g.求:(1)线框竖直方向速度为v1时,线框中瞬时电流的大小;
(2)线框在复合场中运动的最大电功率;
(3)若线框从开始抛出到瞬时速度大小达到v2所经历的时间为t,那么线框在时间t内的总位移大小为多少.

【答案】分析:(1)线框竖直方向速度为v1时,左右两边切割产生的感应电动势抵消,根据法拉第电磁感应定律求上下两边产生的感应电动势.e=△BLv1,△B=k△z=kL.
再由欧姆定律求感应电流.
(2)线框在复合场中运动时,匀速运动时,速度最大,此时重力与磁场力平衡,由平衡条件,结合安培力表达式,求出最大速度.框在复合场中运动的最大电功率与重力功率相等.
(3)线框从抛出到速度v2过程,根据牛顿第二定律: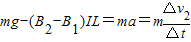 ,得到速度的变化量,再两边求和,运用积分法即可求得总位移大小.
,得到速度的变化量,再两边求和,运用积分法即可求得总位移大小.
解答:解:(1)线框竖直方向速度为v1时,左右两边切割产生的感应电动势抵消,上下两边产生的总感应电动势为:e=△BLv1,
而△B=k△z=kL,则得e=kL2v1
线框中瞬时电流的大小为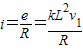 .
.
(2)由线框在复合场中的速度最大时,重力与磁场力平衡得
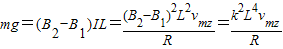
∴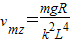
由能量关系得:线框在复合场中运动的最大电功率与重力功率相等,即有
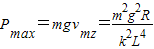
(3)线框从抛出到速度v2过程,由牛顿第二定律得 mg-(B2-B1)IL=ma=m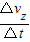
则得 mg△t-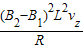 △t=m△vz
△t=m△vz
两边求和得
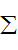 mg△t-
mg△t-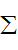
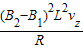 △t=
△t=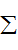 m△vz
m△vz
又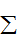 vz△t=△z,B2-B1=kL,
vz△t=△z,B2-B1=kL,
则得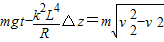
时间t内z方向位移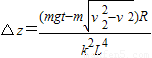
而线框水平所受的安培力的合力为零,所以水平方向做匀速直线运动.则
时间t内线框的总位移大小为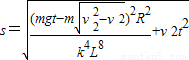
答:
(1)线框竖直方向速度为v1时,线框中瞬时电流的大小为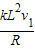 ;
;
(2)线框在复合场中运动的最大电功率是线框在复合场中运动的最大电功率是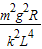 ;
;
(3)若线框从开始抛出到瞬时速度大小达到v2所经历的时间为t,线框在时间t内的总位移大小为为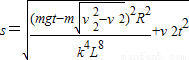 .
.
点评:本题中磁场是非匀强磁场,线框四边都切割磁感线,左右两边电动势抵消,所受的安培力也抵消,根据E=BLv分别得到上下两边的电动势,再求总电动势.本题的难点是运用积分法求竖直方向的位移,其切入口是牛顿第二定律及加速度的定义式.
再由欧姆定律求感应电流.
(2)线框在复合场中运动时,匀速运动时,速度最大,此时重力与磁场力平衡,由平衡条件,结合安培力表达式,求出最大速度.框在复合场中运动的最大电功率与重力功率相等.
(3)线框从抛出到速度v2过程,根据牛顿第二定律:
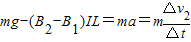 ,得到速度的变化量,再两边求和,运用积分法即可求得总位移大小.
,得到速度的变化量,再两边求和,运用积分法即可求得总位移大小.解答:解:(1)线框竖直方向速度为v1时,左右两边切割产生的感应电动势抵消,上下两边产生的总感应电动势为:e=△BLv1,
而△B=k△z=kL,则得e=kL2v1
线框中瞬时电流的大小为
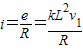 .
.(2)由线框在复合场中的速度最大时,重力与磁场力平衡得
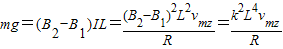
∴
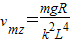
由能量关系得:线框在复合场中运动的最大电功率与重力功率相等,即有
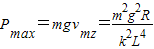
(3)线框从抛出到速度v2过程,由牛顿第二定律得 mg-(B2-B1)IL=ma=m
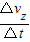
则得 mg△t-
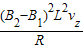 △t=m△vz
△t=m△vz两边求和得
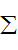 mg△t-
mg△t-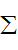
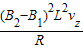 △t=
△t=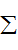 m△vz
m△vz又
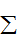 vz△t=△z,B2-B1=kL,
vz△t=△z,B2-B1=kL,则得
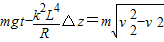
时间t内z方向位移
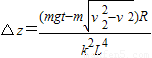
而线框水平所受的安培力的合力为零,所以水平方向做匀速直线运动.则
时间t内线框的总位移大小为
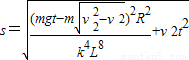
答:
(1)线框竖直方向速度为v1时,线框中瞬时电流的大小为
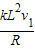 ;
;(2)线框在复合场中运动的最大电功率是线框在复合场中运动的最大电功率是
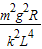 ;
;(3)若线框从开始抛出到瞬时速度大小达到v2所经历的时间为t,线框在时间t内的总位移大小为为
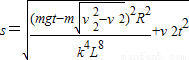 .
.点评:本题中磁场是非匀强磁场,线框四边都切割磁感线,左右两边电动势抵消,所受的安培力也抵消,根据E=BLv分别得到上下两边的电动势,再求总电动势.本题的难点是运用积分法求竖直方向的位移,其切入口是牛顿第二定律及加速度的定义式.

练习册系列答案
相关题目
 如图所示,甲、乙、丙三小球分别位于如图所示的竖直平面内,甲、乙在同一条竖直直线上,甲、丙在同一条水平线上,P点在丙球正下方.某时刻,甲、乙、丙同时开始运动,甲以水平速度v0平抛,乙以水平速度v0沿水平面向右做匀速直线运动,丙做自由落体运动,则下列说法正确的是( )
如图所示,甲、乙、丙三小球分别位于如图所示的竖直平面内,甲、乙在同一条竖直直线上,甲、丙在同一条水平线上,P点在丙球正下方.某时刻,甲、乙、丙同时开始运动,甲以水平速度v0平抛,乙以水平速度v0沿水平面向右做匀速直线运动,丙做自由落体运动,则下列说法正确的是( ) 如图所示,竖直放置的长直导线通以恒定电流,导线右侧充满垂直纸面向内的匀强磁场一矩形线圈与导线在同一平面上.下列情形下线框内能产生感应电流的是( )
如图所示,竖直放置的长直导线通以恒定电流,导线右侧充满垂直纸面向内的匀强磁场一矩形线圈与导线在同一平面上.下列情形下线框内能产生感应电流的是( )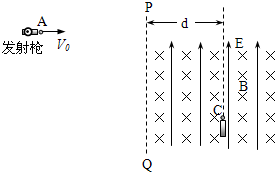 如图所示,竖直平面内,直线PQ右侧足够大的区域内存在竖直向上的匀强电场和垂直于纸面向里的匀强磁场.直线PQ右侧距PQ水平距离为d=28.2cm(计算时取
如图所示,竖直平面内,直线PQ右侧足够大的区域内存在竖直向上的匀强电场和垂直于纸面向里的匀强磁场.直线PQ右侧距PQ水平距离为d=28.2cm(计算时取 如图所示,竖直平面内的轨道.ABC由粗糙的水平轨道AB与光滑的四分之一圆弧轨道BC组成,轨道放在光滑水平面上.一个质量为m的小物块(可视为质点)从轨道A端以初速度v0冲上水平轨道AB,沿着轨道运动到圆弧轨道BC上某点后再沿BC滑下,最后停在永平轨道AB的中点.已知水平轨道AB长为£,轨道ABC的质量为3m.不计空气阻力.求:
如图所示,竖直平面内的轨道.ABC由粗糙的水平轨道AB与光滑的四分之一圆弧轨道BC组成,轨道放在光滑水平面上.一个质量为m的小物块(可视为质点)从轨道A端以初速度v0冲上水平轨道AB,沿着轨道运动到圆弧轨道BC上某点后再沿BC滑下,最后停在永平轨道AB的中点.已知水平轨道AB长为£,轨道ABC的质量为3m.不计空气阻力.求: