题目内容
15. 如图所示,在倾角为α=30°的光滑固定斜面上,有两个质量均为m的小球A?B,它们用劲度系数为k的轻弹簧连接,现对A施加一水平向右的恒力,使A?B均静止在斜面上,下列说法正确的是( )
如图所示,在倾角为α=30°的光滑固定斜面上,有两个质量均为m的小球A?B,它们用劲度系数为k的轻弹簧连接,现对A施加一水平向右的恒力,使A?B均静止在斜面上,下列说法正确的是( )| A. | 弹簧的伸长量为mg/k | B. | 水平恒力大小为$\frac{\sqrt{3}}{3}$mg | ||
| C. | 撤掉恒力的瞬间小球A的加速度为g | D. | 撤掉恒力的瞬间小球B的加速度为g |
分析 先以整体为研究对象,根据平衡条件求出力F的大小;然后根据A处于平衡状态,可以求出弹簧弹力,从而进一步求出弹簧的原长.
解答 解:A、B、以整体为研究对象,受力分析,系统处于平衡状态,沿斜面方向有:
Fcos30°=2mgsin30° …①
解①得F=$\frac{2\sqrt{3}}{3}mg$,
以B为研究对象沿斜面方向有重力沿斜面分析的分力等于弹簧的弹力:
kx=mgsin30° …②
由②得:x=$\frac{mg}{2k}$.故A错误,B错误;
C、D、撤去恒力的瞬间,小球的位置来不及变化,所以弹簧的拉力不变,则小球B的受力不变,所以撤掉恒力的瞬间小球B的加速度为0;
对A进行受力分析如图,则沿斜面向下的方向:ma=mgsin30°+kx=2mgsin30°=mg
所以:a=g,即撤掉恒力的瞬间小球A的加速度为g.故C正确,D错误.
故选:C
点评 对于连接体问题注意整体与隔离法的应用,正确选取研究对象然后受力分析,根据所处状态列方程求解.

练习册系列答案
相关题目
5.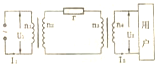 如图所示,远距离输电线路中,升压变压器和降压变压器均为理想变压器,且$\frac{{n}_{2}}{{n}_{1}}$=$\frac{{n}_{3}}{{n}_{4}}$.升压变压器原线圈的电压为U1,原线圈中电流为I1;降压变压器副线圈的电压为U2,副线圈中电流为I2.远距离输电线路上电阻的电压为U额.则下列说法正确的是( )
如图所示,远距离输电线路中,升压变压器和降压变压器均为理想变压器,且$\frac{{n}_{2}}{{n}_{1}}$=$\frac{{n}_{3}}{{n}_{4}}$.升压变压器原线圈的电压为U1,原线圈中电流为I1;降压变压器副线圈的电压为U2,副线圈中电流为I2.远距离输电线路上电阻的电压为U额.则下列说法正确的是( )
 如图所示,远距离输电线路中,升压变压器和降压变压器均为理想变压器,且$\frac{{n}_{2}}{{n}_{1}}$=$\frac{{n}_{3}}{{n}_{4}}$.升压变压器原线圈的电压为U1,原线圈中电流为I1;降压变压器副线圈的电压为U2,副线圈中电流为I2.远距离输电线路上电阻的电压为U额.则下列说法正确的是( )
如图所示,远距离输电线路中,升压变压器和降压变压器均为理想变压器,且$\frac{{n}_{2}}{{n}_{1}}$=$\frac{{n}_{3}}{{n}_{4}}$.升压变压器原线圈的电压为U1,原线圈中电流为I1;降压变压器副线圈的电压为U2,副线圈中电流为I2.远距离输电线路上电阻的电压为U额.则下列说法正确的是( )| A. | U额=U1-U2 | B. | U额>U1-U2 | C. | I1=I2 | D. | I1>I2 |
6.某实验小组用伏安法测量一段金属丝的电阻Rx,实验所用器材为:电池组(电动势3V,内阻约为1Ω)、电流表(内阻约0.1Ω)、电压表(内阻约3KΩ)、滑动变阻器R(0~20Ω,额定电流2A)、开关、导线若干.
(1)该小组同学利用以上器材正确连接好电路,进行实验测量,记录数据如下:
由以上实验数据可知,他们测量Rx是采用下面图中的乙 图(选填“甲”或“乙”).

(2)该小组的同学在坐标纸上建立U-I坐标系,如图丙所示,图中已标出了与测量数据对应的4个坐标点.请在图中标出第2、4、6次测量数据的坐标点,并描绘出U-I图线.由图线得出金属丝的电阻值Rx=4.4Ω(保留两位有效数字).
(3)任何实验测量都存在误差.本实验所用测量仪器均已校准,下列关于本实验中误差的说法中正确的选项是B.
A.由于电流表和电压表内阻引起的误差属于偶然误差
B.用U-I图象处理数据来求金属丝的电阻可以减少偶然误差.
C.由于读数引起的误差属于系统误差
D.若将电流表和电压表的内阻计算在内,可以消除由测量仪表引起的偶然误差.
(1)该小组同学利用以上器材正确连接好电路,进行实验测量,记录数据如下:
| 次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| U/V | 0.10 | 0.30 | 0.70 | 1.00 | 1.50 | 1.70 | 2.30 |
| I/A | 0.020 | 0.060 | 0.160 | 0.220 | 0.340 | 0.460 | 0.520 |

(2)该小组的同学在坐标纸上建立U-I坐标系,如图丙所示,图中已标出了与测量数据对应的4个坐标点.请在图中标出第2、4、6次测量数据的坐标点,并描绘出U-I图线.由图线得出金属丝的电阻值Rx=4.4Ω(保留两位有效数字).
(3)任何实验测量都存在误差.本实验所用测量仪器均已校准,下列关于本实验中误差的说法中正确的选项是B.
A.由于电流表和电压表内阻引起的误差属于偶然误差
B.用U-I图象处理数据来求金属丝的电阻可以减少偶然误差.
C.由于读数引起的误差属于系统误差
D.若将电流表和电压表的内阻计算在内,可以消除由测量仪表引起的偶然误差.
3.下列说法正确的是( )
| A. | 只要知道水的摩尔质量和水分子的质量,就可以计算出阿伏伽德罗常数 | |
| B. | 扩散现象和布朗运动都与温度有关,所以扩散现象和布朗运动都是分子的热运动 | |
| C. | 彩色液晶显示器利用了液晶的光学性质具有各向异性的特点 | |
| D. | 气体对容器的压强是大量气体分子对容器的碰撞引起的,它跟气体分子的密集程度以及气体分子的平均动能有关 |
7. 一定质量的理想气体从状态A经状态B变化到状态C,这一过程在V-T图中表示如图所示,则下述结论错误的是( )
一定质量的理想气体从状态A经状态B变化到状态C,这一过程在V-T图中表示如图所示,则下述结论错误的是( )
 一定质量的理想气体从状态A经状态B变化到状态C,这一过程在V-T图中表示如图所示,则下述结论错误的是( )
一定质量的理想气体从状态A经状态B变化到状态C,这一过程在V-T图中表示如图所示,则下述结论错误的是( )| A. | 在过程AB中,气体压强不断变大 | B. | 在过程BC中,气体密度不断变大 | ||
| C. | 在过程AB中,气体对外界做功 | D. | 在过程BC中,外界对气体做功 |
5.下列说法正确的是( )
| A. | 已知阿伏加德罗常数、气体摩尔质量和密度,可算出该气体分子间的平均距离 | |
| B. | 布朗运动是指悬浮在液体中的固体颗粒的无规则运动 | |
| C. | 给自行车轮胎打气时,打到后面很难打,是因为气体分子间存在斥力的缘固 | |
| D. | 物质是晶体还是非晶体,比较可靠的办法是从各向异性或各向同性来判断 | |
| E. | 热力学第二定律也叫做熵增加原理 |
 如图所示,光滑水平面上滑块A,C'质量均为m=1kg,B质量为M=3kg.开始时A,B静止,C,以初速度v0=2m/s的速度滑向A,与A碰后C的速度变为零,A向右运动与B发生碰撞并粘在一起.
如图所示,光滑水平面上滑块A,C'质量均为m=1kg,B质量为M=3kg.开始时A,B静止,C,以初速度v0=2m/s的速度滑向A,与A碰后C的速度变为零,A向右运动与B发生碰撞并粘在一起.
 如图所示,竖直平面内固定间距为L=0.5m的光滑金属导轨(电阻不计),虚线下方存在垂直于导轨平面的匀强磁场,磁感应强度B=1T.两根质量相同、电阻均为R=1Ω的完全相同金属杆水平放置在导轨上,与导轨接触良好.在磁场外固定杆Ⅰ,在磁场内静止释放杆Ⅱ,经过一段时间后开始匀速运动,速度v=4m/s.求:
如图所示,竖直平面内固定间距为L=0.5m的光滑金属导轨(电阻不计),虚线下方存在垂直于导轨平面的匀强磁场,磁感应强度B=1T.两根质量相同、电阻均为R=1Ω的完全相同金属杆水平放置在导轨上,与导轨接触良好.在磁场外固定杆Ⅰ,在磁场内静止释放杆Ⅱ,经过一段时间后开始匀速运动,速度v=4m/s.求: