题目内容
8.如图甲所示,绝缘轨道ABCD与水平面成37°,除BC部分外其余光滑,在D处垂直斜面固定一绝缘挡板,AB间距L1=3m,BC间距L2=0.6m.一质量m=1kg的玩具(视为质点)可在轨道上沿直线滑行,与挡板碰撞后原速返回,滑行过程中空气阻力不计,重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8.
(1)玩具由A点静止释放,经1.1s到达C点,求玩具与BC间的动摩擦因数;
(2)在B点左侧区域施加竖直向上的匀强电场,电场强度E=2.5×103N/C,如图乙所示.让玩具带上q=-2×10-3C的电量,仍由A点静止释放后.求:
①玩具在滑行过程中的最小加速度amin和最大加速度amax;
②玩具与挡板第一次碰撞后上升的最高位置距A点的距离L3;
(3)在第(2)问的条件下,求玩具从开始释放到停止运动的整个过程中因摩擦产生的总热量Q.
分析 (1)根据牛顿第二定律分别求出AB和BC段的加速度,结合位移时间和速度时间关系即可求出BC段的动摩擦因数;
(2)①进行受力分析,从B到C受力平衡,加速度最小;从C到B加速度最大,根据牛顿第二定律求出最大加速度;
②假设最高点在B点以上,根据能量守恒定律求解,再对结果进行检验;
(3)根据能量守恒定律求出玩具最后停止的位置距B点的距离,再求出摩擦产生的热量;
解答 解:(1)AB段,根据牛顿第二定律$mgsin37°=m{a}_{1}^{\;}$
解得:${a}_{1}^{\;}=gsin37°=6m/{s}_{\;}^{2}$
根据${L}_{1}^{\;}=\frac{1}{2}{a}_{1}^{\;}{t}_{1}^{2}$,得${t}_{1}^{\;}=1s$
B点速度${v}_{B}^{\;}={a}_{1}^{\;}{t}_{1}^{\;}=6m/s$
从B到C的时间${t}_{2}^{\;}=t-{t}_{1}^{\;}=0.1s$
BC间的距离${L}_{2}^{\;}={v}_{B}^{\;}{t}_{2}^{\;}$$+\frac{1}{2}{a}_{2}^{\;}{t}_{2}^{2}$
BC段,根据牛顿第二定律,有
$mgsin37°-μmgcos37°=m{a}_{2}^{\;}$
解得:${a}_{2}^{\;}=g(sin37°-μcos37°)$
解得:${a}_{2}^{\;}=0$,μ=0.75
(2)①f=μ(mg+qE)cos37°=9N
mgsin37°=6N
qEsin37°=3N
从B到C的过程中加速度最小:
据$(mg+qE)sin37°-f=m{a}_{min}^{\;}$,得${a}_{min}^{\;}=0$
由C运行到B的过程中加速度最大:
据$f+(mg+qE)sin37°=m{a}_{max}^{\;}$,得${a}_{max}^{\;}=18m/{s}_{\;}^{2}$
②假定最高点在B点以上,有:$mg{L}_{3}^{\;}sin37°=2f{L}_{2}^{\;}$
代入数据得${L}_{3}^{\;}=1.8m$,因${L}_{3}^{\;}<{L}_{1}^{\;}$,假设成立,结论${L}_{3}^{\;}=1.8m$
(3)假定玩具停在B处,$\frac{mg{L}_{1}^{\;}sin37°}{f{L}_{2}^{\;}}=\frac{18}{5.4}=3+\frac{1}{3}$
可见,玩具应停在BC之间某处,设此处距C点为x,有:
$mg({L}_{1}^{\;}+{L}_{2}^{\;}-x)sin37°+qE({L}_{2}^{\;}-x)sin37°$=$f(3{L}_{2}^{\;}+x)$
代入数据得x=0.4m
所以$Q=f(3{L}_{2}^{\;}+x)=9×2.2=19.8J$
答:(1)玩具与BC间的动摩擦因数为0.75;
(2)①玩具在滑行过程中的最小加速度${a}_{min}^{\;}$为0和最大加速度${a}_{max}^{\;}$为$18m/{s}_{\;}^{2}$;
②玩具与挡板第一次碰撞后上升的最高位置距A点的距离${L}_{3}^{\;}$为1.8m;
(3)在第(2)问的条件下,玩具从开始释放到停止运动的整个过程中因摩擦产生的总热量Q为19.8J
点评 考查动能定理、牛顿第二定律,并让学生知道动能定理过程选取的重要性,同时搞清电场力、重力做功与路径无关,摩擦力做功与路径有关.

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 如图所示为一带电量为q的粒子从x=0处开始,只在电场力作用下沿x轴运动过程中粒子的电势能Ep随x变化的图象.0-x2范围内,图象为曲线;x1-x2范围内,图象为直线.图中所标示的量均已知,则( )
如图所示为一带电量为q的粒子从x=0处开始,只在电场力作用下沿x轴运动过程中粒子的电势能Ep随x变化的图象.0-x2范围内,图象为曲线;x1-x2范围内,图象为直线.图中所标示的量均已知,则( )| A. | 在x=0处,粒子的速度为零 | |
| B. | 在x=x1处,粒子受到的电场力为零 | |
| C. | 在x1到x2区域内,电场沿x轴负方向 | |
| D. | 在x2到x3区域内,电场强度大小为$\frac{{{E_{p1}}}}{{q({x_3}-{x_2})}}$ |
 如图所示,理想变压器为降压变压器,原线圈通过灯泡L1与正弦式交流电相连,副线圈通过导线与两个相同的灯泡L2和L3相连,开始时开关S处于断开状态.当S闭合后,所有灯泡都能发光.下列说法中正确的是( )
如图所示,理想变压器为降压变压器,原线圈通过灯泡L1与正弦式交流电相连,副线圈通过导线与两个相同的灯泡L2和L3相连,开始时开关S处于断开状态.当S闭合后,所有灯泡都能发光.下列说法中正确的是( )| A. | 灯泡L1和L2中的电流有效值可能相等 | |
| B. | 灯泡L2两端的电压变小 | |
| C. | 灯泡L1变亮,灯泡L2的亮度不变 | |
| D. | 变压器原线圈的输入功率不变 |

| A. | 由于B、C、D三点到A点的距离相等,则这三点的电场强度一定相同 | |
| B. | B、C、D三点的电势相等,但过B、C、D三点的平面不是等势面 | |
| C. | 如果将一正的点电荷由D点沿AD方向远离A点,则电场力做负功 | |
| D. | 如果在B、C、D三点放三个合适的点电荷,则A点的电荷所受的电场力可能为零 |
| A. | ${\;}_{92}^{235}$U裂变时释放出大量能量,产生明显的质量亏损,所以核子数要减小 | |
| B. | ${\;}_{92}^{235}$U的一种可能的裂变是变成两个中等质量的原子核,反应方程式为:${\;}_{92}^{235}$U+${\;}_{0}^{1}$n→${\;}_{56}^{141}$Ba+${\;}_{36}^{92}$Kr+2${\;}_{0}^{1}$n | |
| C. | ${\;}_{92}^{235}$U是天然放射性元素,常温下它的半衰期约为45亿年,升高温度半衰期缩短 | |
| D. | 一个${\;}_{92}^{235}$U裂变能放出约200 MeV的能量,相当于3.2×10-11 J |
 一标有“6V 0.5 A”的小型直流电动机,转子由铜导线绕制的线圈组成,阻值约为1Ω.某兴趣小组设汁一个实验测量此电动机线圈的电阻.实验室提供的器材除导线和开关外还有:
一标有“6V 0.5 A”的小型直流电动机,转子由铜导线绕制的线圈组成,阻值约为1Ω.某兴趣小组设汁一个实验测量此电动机线圈的电阻.实验室提供的器材除导线和开关外还有:
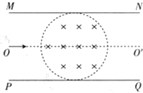 如图所示,平行板MN、PQ间距离为d,板长为2d,板的正中有一半径为$\frac{d}{2}$的圆形有界磁场,磁场边界刚好与两板相切,两板间所加电压为U,一质量为m,电量为q的带电粒子从左端沿两板间的中线向右射入两板间,若只撤去磁场,粒子刚好从上板右端N点射出,若只撤去两板间所加的电压,带电粒子恰好能从下板的右端Q点射出,不计粒子的重力,求:
如图所示,平行板MN、PQ间距离为d,板长为2d,板的正中有一半径为$\frac{d}{2}$的圆形有界磁场,磁场边界刚好与两板相切,两板间所加电压为U,一质量为m,电量为q的带电粒子从左端沿两板间的中线向右射入两板间,若只撤去磁场,粒子刚好从上板右端N点射出,若只撤去两板间所加的电压,带电粒子恰好能从下板的右端Q点射出,不计粒子的重力,求: 做“探究求合力的方法”实验时,先将橡皮条的一端固定在水平木板上,另一端系上带有绳套的两根细绳.实验时,需要两次拉伸橡皮条,一次是通过两细绳用两个弹簧秤互成角度地拉橡皮条,另一次是用一个弹簧秤通过细绳拉橡皮条.
做“探究求合力的方法”实验时,先将橡皮条的一端固定在水平木板上,另一端系上带有绳套的两根细绳.实验时,需要两次拉伸橡皮条,一次是通过两细绳用两个弹簧秤互成角度地拉橡皮条,另一次是用一个弹簧秤通过细绳拉橡皮条.