题目内容
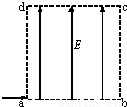
如图所示,长为L(L=ab=dc),高为L(L=bc=ad)的矩形区域abcd内存在着匀强电场.电量为q、质量为m、初速度为v的带电粒子从a点沿ab方向进入电场,不计粒子重力.(1)若粒子从c点离开电场,求电场强度的大小
(2)若粒子从bc边某处离开电场时速度为v,求电场强度的大小
(3)若粒子从cd边某处离开电场时速度为v,求电场强度的大小.
【答案】分析:(1)若粒子从C点离开电场,粒子做类平抛运动沿电场方向上的位移为L,垂直于电场方向上的位移为L,结合牛顿第二定律和运动学公式求出电场强度的大小.
(2)若粒子从bc边某处离开电场时速度为v,根据平行四边形定则求出粒子沿电场方向上的速度,结合牛顿第二定律和速度时间公式求出电场强度的大小.
(3)若粒子从cd边某处离开电场时速度为v,运用动能定理求出电场强度的大小.
解答:解:(1)a→c过程粒子类平抛 沿v方向:L=vt
垂直v方向: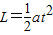
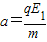
解得: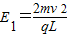
(2)离开电场时垂直v方向: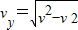
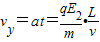
解得: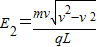
(3)由动能定理: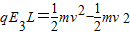
解得: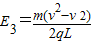
答:(1)若粒子从c点离开电场,电场强度的大小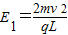 .
.
(2)若粒子从bc边某处离开电场时速度为v,电场强度的大小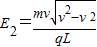 .
.
(3)若粒子从cd边某处离开电场时速度为v,电场强度的大小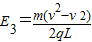 .
.
点评:带电粒子在电场中类平抛运动,沿电场方向上做匀加速直线运动,垂直于电场方向上做匀速直线运动.结合牛顿第二定律和运动学公式进行求解.
(2)若粒子从bc边某处离开电场时速度为v,根据平行四边形定则求出粒子沿电场方向上的速度,结合牛顿第二定律和速度时间公式求出电场强度的大小.
(3)若粒子从cd边某处离开电场时速度为v,运用动能定理求出电场强度的大小.
解答:解:(1)a→c过程粒子类平抛 沿v方向:L=vt
垂直v方向:
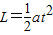
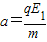
解得:
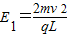
(2)离开电场时垂直v方向:
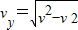
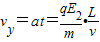
解得:
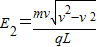
(3)由动能定理:
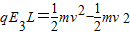
解得:
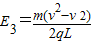
答:(1)若粒子从c点离开电场,电场强度的大小
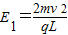 .
.(2)若粒子从bc边某处离开电场时速度为v,电场强度的大小
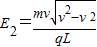 .
.(3)若粒子从cd边某处离开电场时速度为v,电场强度的大小
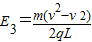 .
.点评:带电粒子在电场中类平抛运动,沿电场方向上做匀加速直线运动,垂直于电场方向上做匀速直线运动.结合牛顿第二定律和运动学公式进行求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,相距为d的两水平虚线和分别是水平向里的匀强磁场的边界,磁场的磁感应强度为B,正方形线框abcd边长为L(L<d)、质量为m.将线框在磁场上方高h处由静止开始释放,当ab边进入磁场时速度为v0,cd边刚穿出磁场时速度也为v0.从ab边刚进入磁场到cd边刚穿出磁场的整个过程中( )
如图所示,相距为d的两水平虚线和分别是水平向里的匀强磁场的边界,磁场的磁感应强度为B,正方形线框abcd边长为L(L<d)、质量为m.将线框在磁场上方高h处由静止开始释放,当ab边进入磁场时速度为v0,cd边刚穿出磁场时速度也为v0.从ab边刚进入磁场到cd边刚穿出磁场的整个过程中( )| A、线框一直都有感应电流 | B、线框产生的热量为mg(d+h+L) | C、线框有一阶段的加速度为g | D、线框作匀减速运动 |
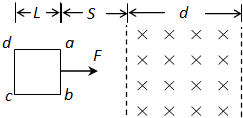 如图所示,光滑绝缘的水平面内有竖直方向的宽度为d的匀强磁场区,磁场的磁感应强度为B.正方形金属线框abcd边长为L(L<d),质量为m,现对线框施加垂直于ab边的水平恒力F使线框从磁场左侧距磁场S处由静止开始运动,如果ab边刚进入磁场时的速度为v0,cd边刚穿出磁场时的速度也为v0,则从ab边刚进入磁场到cd边刚穿出磁场的整个过程( )
如图所示,光滑绝缘的水平面内有竖直方向的宽度为d的匀强磁场区,磁场的磁感应强度为B.正方形金属线框abcd边长为L(L<d),质量为m,现对线框施加垂直于ab边的水平恒力F使线框从磁场左侧距磁场S处由静止开始运动,如果ab边刚进入磁场时的速度为v0,cd边刚穿出磁场时的速度也为v0,则从ab边刚进入磁场到cd边刚穿出磁场的整个过程( )| A、线框有一阶段在做匀加速运动 | B、线框ab边在刚进入磁场时可能做加速运动 | C、线框ab边在刚穿出磁场时一定是先做减速运动 | D、线框中产生的热量为F(d+S+L) |
 如图所示,长为L的细绳上端系一质量不计的环,环套在光滑水平杆上,在细线的下端另一个质量为m的铁球(可视作质点),球离地的高度h=L,当绳受到大小为3mg的拉力时就会断裂.现让环与球一起以
如图所示,长为L的细绳上端系一质量不计的环,环套在光滑水平杆上,在细线的下端另一个质量为m的铁球(可视作质点),球离地的高度h=L,当绳受到大小为3mg的拉力时就会断裂.现让环与球一起以 如图所示,长为L(L=ab=dc),高为L(L=bc=ad)的矩形区域abcd内存在着匀强电场.电量为q、质量为m、初速度为v0的带电粒子从a点沿ab方向进入电场,不计粒子重力.
如图所示,长为L(L=ab=dc),高为L(L=bc=ad)的矩形区域abcd内存在着匀强电场.电量为q、质量为m、初速度为v0的带电粒子从a点沿ab方向进入电场,不计粒子重力. =0.01C/kg,E1=l00N/C,E2=E3=300N/C,β=60,Bl=103T,L=5m L =4m小球与管道间动摩擦因数为μ=0.1,求:
=0.01C/kg,E1=l00N/C,E2=E3=300N/C,β=60,Bl=103T,L=5m L =4m小球与管道间动摩擦因数为μ=0.1,求: