题目内容
5. 设地球半径为R,一物体在地球表面时与地球间的万有引力为F,则当该物体在距离地面高R处时(如图),与地球间的万有引力大小为( )
设地球半径为R,一物体在地球表面时与地球间的万有引力为F,则当该物体在距离地面高R处时(如图),与地球间的万有引力大小为( )| A. | $\frac{1}{2}$F | B. | $\frac{1}{4}$F | C. | 2F | D. | 4F |
分析 根据万有引力定律公式,抓住两物体间距离的变化得出万有引力的变化,从而确定正确的答案.
解答 解:当物体在地球表面时,万有引力F=$G\frac{Mm}{{R}^{2}}$,
当物体在距离地面高度R处时,到地心的距离r=2R,则万有引力$F′=\frac{GMm}{{r}^{2}}=\frac{1}{4}F$,故B正确,A、C、D错误.
故选:B.
点评 解决本题的关键掌握万有引力定律公式,知道影响万有引力大小的因素,注意物体与地球间的距离应该是物体到地心的距离.

练习册系列答案
相关题目
16. 如图,一个原来不带电的半径为r的空心金属球放在绝缘支架上,右侧放置一个电荷量为+Q的点电荷,点电荷到金属球表面的最近距离为2r,下列说法正确的是( )
如图,一个原来不带电的半径为r的空心金属球放在绝缘支架上,右侧放置一个电荷量为+Q的点电荷,点电荷到金属球表面的最近距离为2r,下列说法正确的是( )
 如图,一个原来不带电的半径为r的空心金属球放在绝缘支架上,右侧放置一个电荷量为+Q的点电荷,点电荷到金属球表面的最近距离为2r,下列说法正确的是( )
如图,一个原来不带电的半径为r的空心金属球放在绝缘支架上,右侧放置一个电荷量为+Q的点电荷,点电荷到金属球表面的最近距离为2r,下列说法正确的是( )| A. | 金属球右侧感应出正电荷 | |
| B. | 感应起电后金属球总带电量为-Q | |
| C. | 金属球上的感应电荷在球心处激发的电场强度大小为k$\frac{Q}{9{r}^{2}}$ | |
| D. | 点电荷受到的库仑力大小为k$\frac{{Q}^{2}}{4{r}^{2}}$ |
13.已知地球半径为R、地球质量为M、引力常量为G.则质量为m、离地球球心距离为r的人造卫星受到地球对它的万有引力大小为( )
| A. | F=G$\frac{Mm}{r}$ | B. | F=G$\frac{Mm}{{r}^{2}}$ | C. | F=G$\frac{Mm}{R}$ | D. | F=G$\frac{Mm}{{R}^{2}}$ |
20.由万有引力定律可知,把两质点间的距离增加为原来的2倍时,它们之间的引力变为原来的( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 2倍 | D. | 4倍 |
12. 如图所示,固定的光滑倾斜杆上套有一个质量为m的圆环,圆环与竖直放置的轻质弹簧上端相连,弹簧的下端固定在水平地面上的A 点,开始弹簧恰好处于原长h.现让圆环由静止沿杆滑下,滑到杆的底端(未触及地面)时速度恰好为零,已知当地的重力加速度大小为g.则在圆环下滑的整个过程中( )
如图所示,固定的光滑倾斜杆上套有一个质量为m的圆环,圆环与竖直放置的轻质弹簧上端相连,弹簧的下端固定在水平地面上的A 点,开始弹簧恰好处于原长h.现让圆环由静止沿杆滑下,滑到杆的底端(未触及地面)时速度恰好为零,已知当地的重力加速度大小为g.则在圆环下滑的整个过程中( )
 如图所示,固定的光滑倾斜杆上套有一个质量为m的圆环,圆环与竖直放置的轻质弹簧上端相连,弹簧的下端固定在水平地面上的A 点,开始弹簧恰好处于原长h.现让圆环由静止沿杆滑下,滑到杆的底端(未触及地面)时速度恰好为零,已知当地的重力加速度大小为g.则在圆环下滑的整个过程中( )
如图所示,固定的光滑倾斜杆上套有一个质量为m的圆环,圆环与竖直放置的轻质弹簧上端相连,弹簧的下端固定在水平地面上的A 点,开始弹簧恰好处于原长h.现让圆环由静止沿杆滑下,滑到杆的底端(未触及地面)时速度恰好为零,已知当地的重力加速度大小为g.则在圆环下滑的整个过程中( )| A. | 圆环与弹簧和地球组成的系统机械能守恒 | |
| B. | 弹簧的弹性势能一直在增大 | |
| C. | 圆环的机械能先减小后增大 | |
| D. | 弹簧的弹性势能增大了mgh |
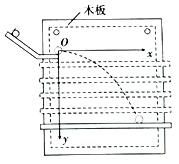 某同学在用如图的装置做“研究平抛物体运动”的实验,已知重力加速度为g,请按要求完成下列填空.
某同学在用如图的装置做“研究平抛物体运动”的实验,已知重力加速度为g,请按要求完成下列填空. 如图所示,用L=1m的细线系着一个小球A组成一个单摆,在悬点O处还固定着另一根竖直的细绳,吊在绳子上的小球B能沿绳子下滑.现将A球拉偏一个很小的角度,B球停在悬点O处,使它们同时开始运动,若A第一次到达最低点时跟B正好相碰,不计A球摩擦阻力,且g≈π2=10m/s2.求:
如图所示,用L=1m的细线系着一个小球A组成一个单摆,在悬点O处还固定着另一根竖直的细绳,吊在绳子上的小球B能沿绳子下滑.现将A球拉偏一个很小的角度,B球停在悬点O处,使它们同时开始运动,若A第一次到达最低点时跟B正好相碰,不计A球摩擦阻力,且g≈π2=10m/s2.求: 如图所示,质量为M的物体位于倾角为45°的固定光滑斜面上,设对物体施加一个水平向右的恒力,其大小和物体所受的重力的大小相等,则物体的加速度a=0m/s2.
如图所示,质量为M的物体位于倾角为45°的固定光滑斜面上,设对物体施加一个水平向右的恒力,其大小和物体所受的重力的大小相等,则物体的加速度a=0m/s2. (1)在做“研究平抛运动”实验时,除了木板、小球、斜槽、铅笔、图钉、坐标纸之外,下列器材中还需要的是D.
(1)在做“研究平抛运动”实验时,除了木板、小球、斜槽、铅笔、图钉、坐标纸之外,下列器材中还需要的是D.