题目内容
如图所示,竖直圆筒内壁光滑,半径为R,顶部有入口A,在A的正下方h处有出口B,一质量为m的小球从入口A沿切线方向由水平槽射入圆筒内,要使球从B处飞出,小球射入口A的速度v0应满足什么条件?在运动过程中,球对筒的压力有多大?

答案:
解析:
解析:
|
解决曲线运动的最基本方法是运动的合成与分解,小球在初速度方向上不受任何力,故小球在水平面内的分运动为匀速率圆周运动;小球在竖直方向无初速度且只受重力,故小球在竖直方向的分运动为自由落体运动.对于周期性的运动问题还要注意多解存在的可能性.圆周运动的周期性决定本题的多解性. 小球自入口A射入后的运动可以分解成两个分运动,一个是以入射速率为线速度在水平面内的匀速圆周运动,另一个是在竖直方向上的自由落体运动,设小球在圆筒内绕过n圈后, 从B处飞出.则小球在水平面内做圆周运动走过的路程是: n(2πR)=v0t(n=1,2,3,…) ① 在竖直方向上有:h= 由①②两式消去t得: v0= 小球在整个运动过程中,水平方向只受支持力FN.FN总是指向圆心,充当向心力.则由牛顿第二定律可知: FN= 由牛顿第三定律可知,小球对筒的压力为 小球射入口A的速度v0应满足v0=2πnR 小球对筒的压力为 |

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
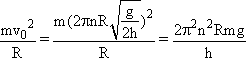 (n=1,2,3,…)
(n=1,2,3,…) 如图所示,竖直圆筒内壁光滑,半径为R,顶部有入口A,在A的正下方h处有出口B,一质量为m的小球从人口A沿圆筒壁切线方向水平射人圆筒内,要使球从B处飞出,小球进入入口A处的速度vo应满足什么条件?
如图所示,竖直圆筒内壁光滑,半径为R,顶部有入口A,在A的正下方h处有出口B,一质量为m的小球从人口A沿圆筒壁切线方向水平射人圆筒内,要使球从B处飞出,小球进入入口A处的速度vo应满足什么条件?
 如图所示,竖直圆筒内壁光滑,半径为R,上部侧面A处开有小孔,在小孔A的正下方h处亦开有与A大小相同的小孔B,小球从小孔A处沿切线方向水平射入筒内,使小球紧贴筒内壁运动,要使小球从B孔处飞出,小球进入A孔的最小速率v0为( )
如图所示,竖直圆筒内壁光滑,半径为R,上部侧面A处开有小孔,在小孔A的正下方h处亦开有与A大小相同的小孔B,小球从小孔A处沿切线方向水平射入筒内,使小球紧贴筒内壁运动,要使小球从B孔处飞出,小球进入A孔的最小速率v0为( )