题目内容
14. 如图所示,相距为d的两条水平虚线L1、L2之间是方向水平向里的匀强磁场,磁感应强度为B,正方形线圈abcd边长为L(L<d),质量为m,电阻为R,将线圈在磁场上方高h处静止释放,cd边刚进入磁场时速度为v0,cd边刚离开磁场时速度也为v0,则线圈从cd边刚进入磁场起一直到ab边离开磁场的过程中,则以下说法中正确的是( )
如图所示,相距为d的两条水平虚线L1、L2之间是方向水平向里的匀强磁场,磁感应强度为B,正方形线圈abcd边长为L(L<d),质量为m,电阻为R,将线圈在磁场上方高h处静止释放,cd边刚进入磁场时速度为v0,cd边刚离开磁场时速度也为v0,则线圈从cd边刚进入磁场起一直到ab边离开磁场的过程中,则以下说法中正确的是( )| A. | 感应电流所做的功为mgd | |
| B. | 线圈下落的最小速度一定为$\sqrt{2g(h+L-d)}$ | |
| C. | 线圈下落的最小速度不可能为$\frac{mgR}{{{B^2}{L^2}}}$ | |
| D. | 线圈进入磁场的时间和穿出磁场的时间不同 |
分析 线圈由静止释放,其下边缘刚进入磁场和刚穿出磁场时刻的速度是相同的,又因为线圈全部进入磁场不受安培力,要做匀加速运动.可知线圈进入磁场先要做减速运动.根据线框的运动情况,分析进入和穿出磁场的时间关系.
解答 解:A、根据能量守恒可知:从cd边刚进入磁场到cd边刚穿出磁场的过程:线圈动能变化量为0,重力势能转化为线框产生的热量,产生的热量 Q=mgd.cd边刚进入磁场时速度为v0,cd边刚离开磁场时速度也为v0,所以线圈穿出磁场与进入磁场的过程运动情况相同,线框产生的热量与从cd边刚进入磁场到cd边刚穿出磁场的过程产生的热量相等,所以线圈从cd边进入磁场到cd边离开磁场的过程,产生的热量Q′=2mgd,感应电流做的功为2mgd,故A错误.
B、线圈全部进入磁场时没有感应电流,不受安培力,做匀加速运动,而cd边刚离开磁场与刚进入磁场时速度相等,所以线圈进磁场时要减速,设线圈的最小速度为vm,可知全部进入磁场的瞬间速度最小.由动能定理,从cd边刚进入磁场到线框完全进入时,则有:$\frac{1}{2}$mvm2-$\frac{1}{2}$mv02=mgL-mgd,有$\frac{1}{2}$mv02=mgh,综上可解得线圈的最小速度为$\sqrt{2g(h+L-d)}$,故B正确;
C、线框可能先做减速运动,在完全进入磁场前做匀速运动,因为完全进入磁场时的速度最小,则mg=$\frac{{B}^{2}{L}^{2}v}{R}$,则线圈下落的最小速度可能为:v=$\frac{mgR}{{B}^{2}{L}^{2}}$,故C错误.
D、cd边刚进入磁场时速度为v0,cd边刚离开磁场时速度也为v0,故知线圈进入磁场和穿出磁场的过程运动情况相同,所用的时间一样,故D错误.
故选:B.
点评 解决本题的关键根据根据线圈下边缘刚进入磁场和刚穿出磁场时刻的速度都是v0,且全部进入磁场将做加速运动,判断出线圈进磁场后先做变减速运动,也得出全部进磁场时的速度是穿越磁场过程中的最小速度.


| A. | 3$\sqrt{2}$A | B. | 3A | C. | 2$\sqrt{3}$A | D. | 3.5A |
 如图所示,一圆形线圈匝数为n,半径为R,线圈平面与匀强磁场垂直,且一半处在磁场中,在△t时间内,磁感应强度的方向不变,大小由B均匀地增大到2B,在此过程中,线圈中产生的感应电动势为( )
如图所示,一圆形线圈匝数为n,半径为R,线圈平面与匀强磁场垂直,且一半处在磁场中,在△t时间内,磁感应强度的方向不变,大小由B均匀地增大到2B,在此过程中,线圈中产生的感应电动势为( )| A. | $\frac{{πB{R^2}}}{2△t}$ | B. | $\frac{{nπB{R^2}}}{△t}$ | C. | $\frac{{nπB{R^2}}}{2△t}$ | D. | $\frac{{2nπB{R^2}}}{△t}$ |
| A. | 撤去电场前后物块的加速度大小之比为1:3 | |
| B. | 电场强度大小为$\frac{2mg}{q}$ | |
| C. | 撤去电场时,物物块的重力势能是$\frac{1}{2}$Ek | |
| D. | 撤去电场时,物块的动能是$\frac{1}{4}$Ek |
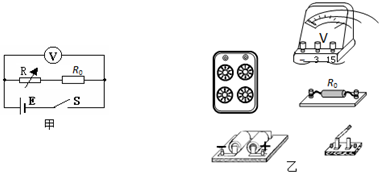
 如图所示,R3=6Ω,电源电动势E=8V,内阻r=1Ω,当S闭合时,标有“4V,4W”的灯泡L正常发光,求:
如图所示,R3=6Ω,电源电动势E=8V,内阻r=1Ω,当S闭合时,标有“4V,4W”的灯泡L正常发光,求: 如图所示,质量M=8kg的小车放在水平光滑的平面上,在小车左端加一水平推力F=8N,当小车向右运动的速度达到1.5m/s时,在小车前端轻轻地放上一个大小不计,质量为m=2kg的小物块,物块与小车间的动摩擦因数μ=0.2,小车足够长.求:
如图所示,质量M=8kg的小车放在水平光滑的平面上,在小车左端加一水平推力F=8N,当小车向右运动的速度达到1.5m/s时,在小车前端轻轻地放上一个大小不计,质量为m=2kg的小物块,物块与小车间的动摩擦因数μ=0.2,小车足够长.求: 如图所示,小球质量为m,轻绳1水平,轻绳2长L,与竖直方向的夹角为θ.则在剪短绳1的瞬间,绳2的张力大小为mgcosθ,小球的加速度大小为gsinθ.
如图所示,小球质量为m,轻绳1水平,轻绳2长L,与竖直方向的夹角为θ.则在剪短绳1的瞬间,绳2的张力大小为mgcosθ,小球的加速度大小为gsinθ.