题目内容
17. 供电局某工程队在冬天架设电线,如图所示,铜导线总质量为M,电线架设好后,电线在杆上固定瓷瓶处的切线方向与竖直方向的夹角为θ.问:
供电局某工程队在冬天架设电线,如图所示,铜导线总质量为M,电线架设好后,电线在杆上固定瓷瓶处的切线方向与竖直方向的夹角为θ.问:(1)杆上瓷瓶处的电线张力F为多大?
(2)最低点处的电线张力F′为多大?
分析 直接对左半边的电线进行受力分析,受重力、与竖直方向成θ角的拉力、水平向右的拉力,然后根据平衡条件并结合正交分解法列式求解即可.
解答 解:对左半边电线受力分析,如图:
由平衡条件得
Fcosθ=$\frac{G}{2}$,
Fsinθ=F′,
解得:
F=$\frac{Mg}{2cosθ}$,
F′=$\frac{1}{2}Mgtanθ$;
答:(1)杆上瓷瓶处的电线张力F为$\frac{Mg}{2cosθ}$;
(2)最低点处的电线张力F′为$\frac{1}{2}Mgtanθ$.
点评 本题关键是先对物体受力分析,然后根据平衡条件并运用正交分解法列式求解,对于三个不平行的力,若合力为零,一定是共点力.

练习册系列答案
相关题目
8.下列关于电场的叙述中正确的是( )
| A. | 以点电荷为圆心,r为半径的球面上,各点的场强都相同 | |
| B. | 正电荷周围的场强一定比负电荷周围的场强大 | |
| C. | 电场中某点的试探电荷电荷量变为原来两倍,该试探电荷所受电场力不变 | |
| D. | 电荷在电场中某点所受电场力的方向与该点电场的方向可能相反 |
5. 如图所示,一楔形斜面体置于水平地面上,斜面的倾角为30°,物块A置于斜面上,用轻弹簧、细绳跨过定滑轮与物块B连接,弹簧轴线与斜面平行,A、B均处于静止状态,已知物块A、B受到的重力分别为10N和5N,不计滑轮与细绳间的摩擦,则下列说法正确的是( )
如图所示,一楔形斜面体置于水平地面上,斜面的倾角为30°,物块A置于斜面上,用轻弹簧、细绳跨过定滑轮与物块B连接,弹簧轴线与斜面平行,A、B均处于静止状态,已知物块A、B受到的重力分别为10N和5N,不计滑轮与细绳间的摩擦,则下列说法正确的是( )
 如图所示,一楔形斜面体置于水平地面上,斜面的倾角为30°,物块A置于斜面上,用轻弹簧、细绳跨过定滑轮与物块B连接,弹簧轴线与斜面平行,A、B均处于静止状态,已知物块A、B受到的重力分别为10N和5N,不计滑轮与细绳间的摩擦,则下列说法正确的是( )
如图所示,一楔形斜面体置于水平地面上,斜面的倾角为30°,物块A置于斜面上,用轻弹簧、细绳跨过定滑轮与物块B连接,弹簧轴线与斜面平行,A、B均处于静止状态,已知物块A、B受到的重力分别为10N和5N,不计滑轮与细绳间的摩擦,则下列说法正确的是( )| A. | 弹簧对A的拉力大小为5N | B. | 斜面对A的支持力大小为5N | ||
| C. | 地面对斜面的摩擦力大小5N | D. | 斜面对A的摩擦力为0 |
12.河北省藁城中学在今年的秋季运动会中,高一某班的某同学创造了100m和200m短跑项目的学校纪录,他的成绩分别是10.84s和21.80s.关于该同学的叙述正确的是( )
| A. | 该同学100 m的平均速度约为9.23 m/s | |
| B. | 该同学在100 m和200 m短跑中,位移分别是100 m和200 m | |
| C. | 该同学的200 m短跑的平均速度约为9.17 m/s | |
| D. | 该同学起跑阶段加速度与速度都为零 |
9.某同学在“用打点计时器测速度”的实验中,用打点计时器记录了被小车拖动的纸带的运动情况,在纸带上确定出A、B、C、D、E、F、G共7个计数点.其相邻点间的距离如图1所示,每两个相邻的测量点之间的时间间隔为0.10s.(本题计算结果均保留3位有效数字)

(1)在实验中,使用打点计时器操作步骤应先接通电源再释放纸带(填“释放纸带”或“接通电源”);
(2)每两个计数点间还有4个点没有标出;
(3)试根据纸带上各个计数点间的距离,每隔0.10s测一次速度,计算出打下B、C、D三个点时小车的瞬时速度,并将各个速度值填入表:
(4)如果打A点时开始计时,将B、C、D、E、F各个时刻的瞬时速度标在如图2所示的直角坐标系中,并画出小车的瞬时速度随时间变化的关系图线.

(1)在实验中,使用打点计时器操作步骤应先接通电源再释放纸带(填“释放纸带”或“接通电源”);
(2)每两个计数点间还有4个点没有标出;
(3)试根据纸带上各个计数点间的距离,每隔0.10s测一次速度,计算出打下B、C、D三个点时小车的瞬时速度,并将各个速度值填入表:
| vB | vC | vD | vE | vF | |
| 数值(m/s) | 0.640 | 0.721 |
6. 如图所示,一个带电油滴从O点以速度v向右上方射入匀强电场中,v的方向与电场方向成α角.若测得油滴到达运动轨迹的最高点P时,它的速度大小仍为v,则下列说法正确的是( )
如图所示,一个带电油滴从O点以速度v向右上方射入匀强电场中,v的方向与电场方向成α角.若测得油滴到达运动轨迹的最高点P时,它的速度大小仍为v,则下列说法正确的是( )
 如图所示,一个带电油滴从O点以速度v向右上方射入匀强电场中,v的方向与电场方向成α角.若测得油滴到达运动轨迹的最高点P时,它的速度大小仍为v,则下列说法正确的是( )
如图所示,一个带电油滴从O点以速度v向右上方射入匀强电场中,v的方向与电场方向成α角.若测得油滴到达运动轨迹的最高点P时,它的速度大小仍为v,则下列说法正确的是( )| A. | P点一定在O点的右上方 | |
| B. | OP与初速度v所成的角度可能为$\frac{α}{2}$ | |
| C. | 油滴到达最高点时,电场力对小球做功的瞬时功率为0 | |
| D. | 油滴到达最高点的过程,电场力对小球一定做正功 |
7. 如图所示,飞船从轨道1变轨至轨道2.若飞船在两轨道上都做匀速圆周运动,不考虑质量变化,相对于在轨道1上,飞船在轨道2上的( )
如图所示,飞船从轨道1变轨至轨道2.若飞船在两轨道上都做匀速圆周运动,不考虑质量变化,相对于在轨道1上,飞船在轨道2上的( )
 如图所示,飞船从轨道1变轨至轨道2.若飞船在两轨道上都做匀速圆周运动,不考虑质量变化,相对于在轨道1上,飞船在轨道2上的( )
如图所示,飞船从轨道1变轨至轨道2.若飞船在两轨道上都做匀速圆周运动,不考虑质量变化,相对于在轨道1上,飞船在轨道2上的( )| A. | 速度大 | B. | 向心加速度大 | C. | 运行周期长 | D. | 角速度小 |
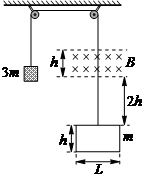 如图所示,质量为3m的重物与一质量为m的线框用一根绝缘细线连接起来,挂在两个高度相同的定滑轮上,已知线框电阻为R,横边边长为L,水平方向匀强磁场的磁感应强度为B,磁场上下边界的距离、线框竖直边长均为h.初始时刻,磁场的下边缘和线框上边缘的高度差为2h,将重物从静止开始释放,线框穿出磁场前,若线框已经做匀速直线运动,滑轮质量、摩擦阻力均不计.求:
如图所示,质量为3m的重物与一质量为m的线框用一根绝缘细线连接起来,挂在两个高度相同的定滑轮上,已知线框电阻为R,横边边长为L,水平方向匀强磁场的磁感应强度为B,磁场上下边界的距离、线框竖直边长均为h.初始时刻,磁场的下边缘和线框上边缘的高度差为2h,将重物从静止开始释放,线框穿出磁场前,若线框已经做匀速直线运动,滑轮质量、摩擦阻力均不计.求: 如图所示,用销钉固定的导热活塞把水平放置的导热汽缸分隔成容积相同的两部分,分别封闭着A、B两部分理想气体:A部分气体压强为pA=2.0×105 Pa,B部分气体压强为pB=1.5×105 Pa.现拔去销钉,待活塞重新稳定后,求此时A部分气体体积与原来体积之比.(外界温度保持不变,活塞与汽缸间摩擦可忽略不计,整个过程无漏气发生)
如图所示,用销钉固定的导热活塞把水平放置的导热汽缸分隔成容积相同的两部分,分别封闭着A、B两部分理想气体:A部分气体压强为pA=2.0×105 Pa,B部分气体压强为pB=1.5×105 Pa.现拔去销钉,待活塞重新稳定后,求此时A部分气体体积与原来体积之比.(外界温度保持不变,活塞与汽缸间摩擦可忽略不计,整个过程无漏气发生)