题目内容
12. 一根张紧的水平弹性长绳上的a、b两点,相距14m,b点在a点的右方,如图所示.当一列简谐横波沿此长绳向右传播时,若a点的位移达到正极大时,b点的位移恰为零,且向下运动,λ>14m.经过1.00s后,a点的位移为零,且向下运动,求这列波的波速.
一根张紧的水平弹性长绳上的a、b两点,相距14m,b点在a点的右方,如图所示.当一列简谐横波沿此长绳向右传播时,若a点的位移达到正极大时,b点的位移恰为零,且向下运动,λ>14m.经过1.00s后,a点的位移为零,且向下运动,求这列波的波速.
分析 根据题意,当简谐横波沿长绳向右传播时,若a点的位移达到正最大时,b点的位移恰为零且向下运动,结合波形,得到a,b两点与波长关系的通项式.又据题意,经过1.00s后a点的位移为零,且向下运动,而b点的位移恰达到负最大,得到时间与周期的关系通项式,求出波速的通项式,再研究波速的特殊值.
解答 解:据“一列简谐横波沿此长绳向右传播时,若a点位移达正极大时,b点的位移恰为零,且向下运动”,可得出此时a、b间的最简波形,得$\frac{3}{4}λ=ab=14$m
因所给定时间与周期的关系未知,故运动时间存在“周期性”.
即$(n+\frac{1}{4})T=△t=1.00$s (n=0,1,2,…)
因此可能的波速为:
$v=\frac{λ}{T}=\frac{14(n+1)}{3}$m/s (n=0,1,2,…)
答:该波的波速可能为$\frac{14(n+1)}{3}$m/s,(n═0,1,2,…)
点评 此题是波的多解题,首先判断波的传播方向,其次,根据波形及传播方向,列出波沿不同方向传播时可能传播距离和周期的通式,再次,看质点间隐含的不同波长的关系,列出波长的通式,再分别将n=0,1,2…代入通式可求得所有可能的答案,要防止漏解或用特解代通解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.下列描述中正确的是( )
| A. | 相对论和量子力学的出现说明人类对自然界的认识更加广泛和深入,那么经典力学就失去了它的意义 | |
| B. | 交流感应电动机就是利用电磁阻尼的原理工作的 | |
| C. | 地磁场在北半球的上空有垂直于地表向上的磁场分量 | |
| D. | 电流通过纯电阻电路做功时,电能全部转化为该电路的内能 |
2.下列关于说法正确的是( )


| A. | 核反应方程${\;}_{92}^{238}$U→${\;}_{90}^{234}$Th+${\;}_{2}^{4}$He为重核裂变,反应过程中会释放能量 | |
| B. | 图是反映铀核衰变的特性曲线,由图可知,经过4860年,铀经历了3个半衰期 | |
| C. | 原子核内部某个质子转变为中子时,放出β射线 | |
| D. | 用能量等于氘核结合能的光子照射静止的氘核,不可能使氘核分解为一个质子和一个中子 |
 如图所示,等腰三角形OPQ区域内存在场强方向沿PQ方向、大小为E的匀强电场,A为PQ的中点,D为OQ的中点,PQ=2L,θ=30°.一质量为m、电量为 q的带正电粒子(重力不计、初速度视为零),从靠近M板O′处由静止释放,经两平行金属板M、N间的电场加速后,通过N板上的小孔沿AO方向从A点射入三角形OPQ区域,粒子恰好从D点射出电场.
如图所示,等腰三角形OPQ区域内存在场强方向沿PQ方向、大小为E的匀强电场,A为PQ的中点,D为OQ的中点,PQ=2L,θ=30°.一质量为m、电量为 q的带正电粒子(重力不计、初速度视为零),从靠近M板O′处由静止释放,经两平行金属板M、N间的电场加速后,通过N板上的小孔沿AO方向从A点射入三角形OPQ区域,粒子恰好从D点射出电场.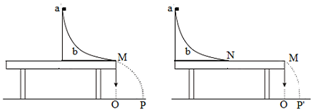
 (1)在“验证机械能守恒定律”实验中,打出的纸带如图所示.设重锤质量为m、交流电周期为T,则打点4时重锤的动能可以表示为$\frac{{m{(h}_{5}{-h}_{3})}^{2}}{{8T}^{2}}$.(用T.m和h1h2h3h4h5表示)
(1)在“验证机械能守恒定律”实验中,打出的纸带如图所示.设重锤质量为m、交流电周期为T,则打点4时重锤的动能可以表示为$\frac{{m{(h}_{5}{-h}_{3})}^{2}}{{8T}^{2}}$.(用T.m和h1h2h3h4h5表示) 在“探究弹力与弹簧伸长的关系”的实验中,某实验小组将不同数量的钩码分别挂在竖直弹簧下端,进行测量,根据实验所测数据,利用描点法作出了所挂钩码的重力G与弹簧总长L的关系图象,如图所示,根据图象回答以下问题:
在“探究弹力与弹簧伸长的关系”的实验中,某实验小组将不同数量的钩码分别挂在竖直弹簧下端,进行测量,根据实验所测数据,利用描点法作出了所挂钩码的重力G与弹簧总长L的关系图象,如图所示,根据图象回答以下问题: