题目内容
如图所示的直角坐标系第 I、I I象限内存在方向向里的匀强磁场，磁感应强度大小B=0.5T，处于坐标原点O的放射源不断地放射出比荷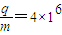
C/kg的正离子，不计离子之间的相互作用．（1）求离子在匀强磁场中运动周期；
（2）若某时刻一群离子自原点O以不同速率沿x轴正方向射出，求经过
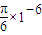s时间这些离子所在位置构成的曲线方程；（3）若离子自原点O以相同的速率v=2.0×106m/s沿不同方向射入第 I象限，要求这些离子穿过磁场区域后都能平行于y轴并指向y轴正方向运动，则题干中的匀强磁场区域应怎样调整（画图说明即可）？并求出调整后磁场区域的最小面积．
【答案】分析：根据洛伦兹力提供向心力，和牛顿第二定律可以求出粒子运动的周期；
粒子运动的周期与粒子的速度无关，运动的时间相等时，所有粒子转过的角度是相等的，这样就可以求得粒子的位置；
根据洛伦兹力提供向心力，求得粒子的运动半径；根据初速度的方向与半径，即可以确定粒子运动的圆心的位置．
解答：解：
（1）洛伦兹力提供向心力，根据牛顿第二定律 有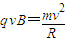
运动周期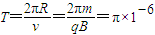
s
（2）离子运动时间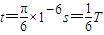
根据左手定则，离子沿逆时针方向作半径不同的圆周运动，
转过的角度均为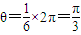
这些离子所在位置均在过坐标原点的同一条直线上，
该直线方程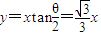
（3）离子自原点O以相同的速率v沿不同方向射入第一象限磁场，均做逆时针方向的匀速圆周运动
根据牛顿第二定律 有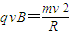
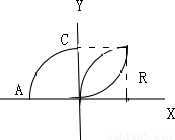
得：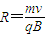
=1m
这些离子的轨道圆心均在第二象限的四分之一圆弧AC上，欲使离子穿过磁场区域后都能平行于y轴并指向y轴正方向运动，离开磁场时的位置在以点（1，0）为圆心、半径R=1m的四分之一圆弧（从原点O起顺时针转动90°）上，磁场区域为两个四分之一圆的交集，如图所示调整后磁场区域的最小面积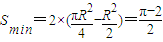
m2
答：（1）离子在匀强磁场中运动周期π×10-6s；
（2）离子所在位置构成的曲线方程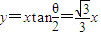
；
（3）调整后磁场区域的最小面积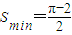
．
点评：该题考查带电粒子在匀强磁场中的运动，难度在第三问，要根据洛伦兹力提供向心力，求得粒子的运动半径；根据初速度的方向与半径，即可以确定粒子运动的圆心的位置．
粒子运动的周期与粒子的速度无关，运动的时间相等时，所有粒子转过的角度是相等的，这样就可以求得粒子的位置；
根据洛伦兹力提供向心力，求得粒子的运动半径；根据初速度的方向与半径，即可以确定粒子运动的圆心的位置．
解答：解：
（1）洛伦兹力提供向心力，根据牛顿第二定律 有
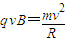
运动周期
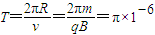s（2）离子运动时间
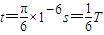
根据左手定则，离子沿逆时针方向作半径不同的圆周运动，
转过的角度均为
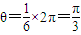
这些离子所在位置均在过坐标原点的同一条直线上，
该直线方程
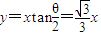
（3）离子自原点O以相同的速率v沿不同方向射入第一象限磁场，均做逆时针方向的匀速圆周运动
根据牛顿第二定律 有
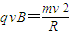
得：
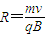=1m 这些离子的轨道圆心均在第二象限的四分之一圆弧AC上，欲使离子穿过磁场区域后都能平行于y轴并指向y轴正方向运动，离开磁场时的位置在以点（1，0）为圆心、半径R=1m的四分之一圆弧（从原点O起顺时针转动90°）上，磁场区域为两个四分之一圆的交集，如图所示调整后磁场区域的最小面积
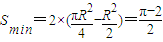m2答：（1）离子在匀强磁场中运动周期π×10-6s；
（2）离子所在位置构成的曲线方程
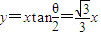；（3）调整后磁场区域的最小面积
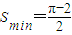．点评：该题考查带电粒子在匀强磁场中的运动，难度在第三问，要根据洛伦兹力提供向心力，求得粒子的运动半径；根据初速度的方向与半径，即可以确定粒子运动的圆心的位置．
练习册系列答案
相关题目
如图所示的直角坐标系中，在y≥0的区域有一垂直于xoy平面的匀强磁场，在第四象限内有一平行于x轴方向的匀强电场．现使一个质量为m，电荷为+q的带电粒子，从坐标原点O以速度v0沿着y轴力向射入匀强磁场，带电粒子从P（x，0）点射出磁场又从Q（0，-y）点射出匀强电场，射出电场时粒子速度跟y轴夹角120°．（不计粒子重力）求：
如图所示的直角坐标系xOy中，x＜0，y＞0的区域内有沿x轴正方向的匀强电场，x≥0的区域内有垂直于xOy坐标平面向外的匀强磁场，x轴上P点坐标为（-L，0），y轴上M点的坐标为（0，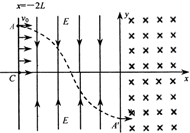
如图所示的直角坐标系中，第Ⅰ、Ⅳ象限内存在着垂直纸面向里的匀强磁场，在x=-2L与y轴之间第Ⅱ、Ⅲ象限内存在大小相等，方向相反的匀强电场，场强方向如图所示．在A（-2L，L）到C（-2L，0）的连线上连续分布着电量为+q、质量为m的粒子．从t=0时刻起，这些带电粒子依次以相同的速度ν沿x轴正方向射出．从A点射入的粒子刚好沿如图所示的运动轨迹从y轴上的A′（0，-L）沿x轴正方向穿过y轴．不计粒子的重力及它们间的相互作用，不考虑粒子间的碰撞．
空间中有一匀强电场，在电场中建立如图所示的直角坐标系o-xyz，M，N为电场中的两个点．M点坐标为（0，-a，0），N点坐标为（