题目内容
7.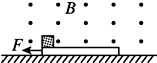 如图所示,空间有一垂直于纸面的磁感应强度为0.5T的匀强磁场,一质量为0.2kg且足够长的绝缘木板静止在光滑水平面上,在木板左端无初速度放置一质量为0.1kg、电荷量q=+0.2C的滑块,滑块与绝缘木板之间的动摩擦因数为0.5,滑块受到的最大静摩擦力可认为等于滑动摩擦力.t=0时对木板施加方向水平向左,大小F=0.6N,方向水平向左的恒力开始作用于木板,g取10m/s2,则( )
如图所示,空间有一垂直于纸面的磁感应强度为0.5T的匀强磁场,一质量为0.2kg且足够长的绝缘木板静止在光滑水平面上,在木板左端无初速度放置一质量为0.1kg、电荷量q=+0.2C的滑块,滑块与绝缘木板之间的动摩擦因数为0.5,滑块受到的最大静摩擦力可认为等于滑动摩擦力.t=0时对木板施加方向水平向左,大小F=0.6N,方向水平向左的恒力开始作用于木板,g取10m/s2,则( )| A. | 木板和滑块一直做加速度为2m/s2的匀加速运动 | |
| B. | 滑块最后做速度为10 m/s的匀速运动 | |
| C. | 木板先做加速度增大的加速运动,最后做加速度大小为3 m/s2的匀加速运动 | |
| D. | t=3s后滑块与木板有发生相对运动 |
分析 先求出木块静摩擦力能提供的最大加速度,再根据牛顿第二定律判断当0.6N的恒力作用于木板时,系统一起运动的加速度,当滑块获得向左运动的速度以后又产生一个方向向上的洛伦兹力,当洛伦兹力等于滑块重力时滑块与木板之间的弹力为零,此时静摩擦力等于零,此后滑块做匀速运动,木板做匀加速直线运动.
解答 解:AB、开始时刻,以木板与滑块整体为研究对象,则在水平方向:F=(M+m)a
代入数据得:a=2m/s2
滑块向左做加速运动,由左手定则可知,受到的洛伦兹力的方向向上,当洛伦兹力的大小与重力大小相等时,滑块将离开木板做匀速直线运动,速度最大,故:qvB=mg
代入数据得:v=10m/s
故A错误,B正确;
C、滑块与绝缘木板之间的动摩擦因数为0.5,则最大静摩擦力约为:
fmax=μmg=0.5×0.1×10=0.5N
滑块随木板做加速运动,开始时的摩擦力:
f=ma=0.1×2=0.2N<0.5N
可知只有当滑块与木板之间的摩擦力小于0.2N时,滑块的加速度才能开始减小,所以滑块先做匀加速直线运动,再做加速度减小的变加速运动,最后做匀速运动;
木板先做加速度增加的加速运动,最后是匀加速直线运动,木板最后的加速度为:
a=$\frac{F}{M}=\frac{0.6N}{0.2kg}=3m/{s}^{2}$;故C正确;
D、当滑块受到的摩擦力是0.2N时,则:f=μN
所以:N=$\frac{f}{μ}$=$\frac{0.2}{0.5}$=0.4N
又:N+qv′B=mg
v′=at′
代入数据得:v′=6m/s,t′=3s
可知t=3s后滑块和木板有相对运动.故D正确.
故选:BCD
点评 本题主要考查了牛顿第二定律的直接应用,要求同学们能正确分析木板和滑块的受力情况,进而判断运动情况.

练习册系列答案
相关题目
17.关于静电场的电场强度和电势,下列说法正确的是( )
| A. | 电场强度的方向处处与等势面垂直 | |
| B. | 电场强度为零的地方,电势也为零 | |
| C. | 随着电场强度的大小逐渐减小,电势也逐渐降低 | |
| D. | 任一点的电场强度总是指向该点电势的升高方向 |
18. 如图所示的真空环境中,匀强磁场方向水平、垂直纸面向外,磁感应强度B=2.5T;匀强电场方向水平向左,场强E=$\sqrt{3}$N/C.一个带负电的小颗粒质量m=3.0×10-7kg,带电荷量q=3.0×10-6C,带电小颗粒在这个区域中刚好做匀速直线运动.(g取10m/s2).则( )
如图所示的真空环境中,匀强磁场方向水平、垂直纸面向外,磁感应强度B=2.5T;匀强电场方向水平向左,场强E=$\sqrt{3}$N/C.一个带负电的小颗粒质量m=3.0×10-7kg,带电荷量q=3.0×10-6C,带电小颗粒在这个区域中刚好做匀速直线运动.(g取10m/s2).则( )
 如图所示的真空环境中,匀强磁场方向水平、垂直纸面向外,磁感应强度B=2.5T;匀强电场方向水平向左,场强E=$\sqrt{3}$N/C.一个带负电的小颗粒质量m=3.0×10-7kg,带电荷量q=3.0×10-6C,带电小颗粒在这个区域中刚好做匀速直线运动.(g取10m/s2).则( )
如图所示的真空环境中,匀强磁场方向水平、垂直纸面向外,磁感应强度B=2.5T;匀强电场方向水平向左,场强E=$\sqrt{3}$N/C.一个带负电的小颗粒质量m=3.0×10-7kg,带电荷量q=3.0×10-6C,带电小颗粒在这个区域中刚好做匀速直线运动.(g取10m/s2).则( )| A. | 这个带电小颗粒一定沿与水平方向成30°向右下方做匀速直线运动 | |
| B. | 若小颗粒运动到图中P点时,把磁场突然撤去,小颗粒将做匀加速直线运动 | |
| C. | 这个带电小颗粒做匀速直线运动的速度大小为0.4 m/s | |
| D. | 这个带电小颗粒做匀速直线运动的速度大小为0.8 m/s |
15. 静止在湖面的小船上有两个人分别向相反方向抛出质量相同的小球,甲向左抛,乙向右抛,如图所示,甲先抛,乙后抛,抛出后两小球相对地的速率相等,则下列说法中正确的是( )
静止在湖面的小船上有两个人分别向相反方向抛出质量相同的小球,甲向左抛,乙向右抛,如图所示,甲先抛,乙后抛,抛出后两小球相对地的速率相等,则下列说法中正确的是( )
 静止在湖面的小船上有两个人分别向相反方向抛出质量相同的小球,甲向左抛,乙向右抛,如图所示,甲先抛,乙后抛,抛出后两小球相对地的速率相等,则下列说法中正确的是( )
静止在湖面的小船上有两个人分别向相反方向抛出质量相同的小球,甲向左抛,乙向右抛,如图所示,甲先抛,乙后抛,抛出后两小球相对地的速率相等,则下列说法中正确的是( )| A. | 两球抛出后,船往左以一定速度运动 | |
| B. | 两球抛出后,船往右以一定速度运动 | |
| C. | 两球抛出后,船的速度先向右再向左 | |
| D. | 两球抛出后,船的速度为零 |
2.我国新研制的液氧煤油发动机新型运载火箭长征六号,于太原卫星发射中心以一箭多星的方式成功发射20颗小卫星.假设其中有两颗卫星A、B轨道平面完全重合、且轨道都是圆形;A卫星运行周期为T1,轨道半径为r1,线速度为v1;B卫星运行周期为T2,轨道半径为r2,线速度为v2,且r1>r2;地球自转周期为T0,引力常量为G,下列说法正确的是( )
| A. | 卫星A、B在轨道上运行时处于完全失重状态,不受任何力的作用 | |
| B. | A卫星的向心加速度为$\frac{{2π{v_1}}}{T_1}$ | |
| C. | 某一时刻卫星A、B在轨道上相距最近,从该时刻每经过$\frac{{{T_1}{T_2}}}{{{T_1}-{T_2}}}$时间,卫星A、B在轨道再次相距最近 | |
| D. | 地球的质量为$\frac{v_2^2r_2^3}{G}$ |
4.一辆车身长度为4.7m的汽车,以72km/h的速度匀速行驶,当车身前端距停止线40m时,司机发现红灯还有3秒结束,此时若( )
| A. | 汽车继续匀速行驶,在红灯熄灭前未通过停止线 | |
| B. | 汽车以4m/s2减速行驶,在红灯熄灭前汽车尚未到达停止线 | |
| C. | 汽车以4m/s2减速行驶,在红灯熄灭前汽车前端已经越过停止线 | |
| D. | 汽车以4m/s2减速行驶,在红灯熄灭前汽车尾部已经越过停止线 |
5.在国际单位制(简称SI)中,力学和电学的基本单位有:m(米)、kg(千克)、s(秒)、A(安培).导出单位Wb(韦伯)表示为( )
| A. | kg•m2•A-1•s-4 | B. | kg•m2•A-1•s-3 | C. | kg•m2•A-1•s-2 | D. | kg•m2•A-1•s-1 |
 物体的质量为100kg,斜面长度l=1.5m,动摩擦因数μ=0.2,α=37°,物体从斜面顶端滑到底端,求:
物体的质量为100kg,斜面长度l=1.5m,动摩擦因数μ=0.2,α=37°,物体从斜面顶端滑到底端,求: 如图所示,在雷雨天气,在一不规则带电云团A附近的B点放置一个q1=-2.0×10-8 C的电荷,若测出它受到的电场力大小为F=4.0×10-6 N,方向如图所示,求:
如图所示,在雷雨天气,在一不规则带电云团A附近的B点放置一个q1=-2.0×10-8 C的电荷,若测出它受到的电场力大小为F=4.0×10-6 N,方向如图所示,求: