题目内容
18.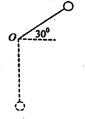 如图所示,一端固定在O点的细线另一端系着一金属小球,小球的质量为m,细线长为l,让细线从偏离水平方向30°的位置由静止释放,已知重力加速度g=10m/s2.求:
如图所示,一端固定在O点的细线另一端系着一金属小球,小球的质量为m,细线长为l,让细线从偏离水平方向30°的位置由静止释放,已知重力加速度g=10m/s2.求:(1)细线刚拉紧时的速度大小;
(2)小球运动到最低点A时绳子受到的拉力是多大?
分析 (1)小球从开始下落到细线绷紧前做自由落体运动,遵守机械能守恒,根据机械能守恒定律可求解细线刚拉紧时的速度大小;
(2)细线绷紧瞬间沿细线方向的速度突然减至零,只有垂直于细线的分速度,将速度分解得到圆周运动的初速度,再机械能守恒求得小球运动到最低点A时的速度,由牛顿第二定律求解拉力.
解答 解:(1)小球先做自由落体运动,设细线刚拉紧时的速度大小为v1.根据机械能守恒定律得:
mgl=$\frac{1}{2}m{v}_{1}^{2}$
解得 v1=$\sqrt{2gl}$
(2)拉紧细线后瞬间,小球的速度设为v2,根据运动的分解得:
v2=v1cos30°=$\sqrt{\frac{3}{2}gl}$
设小球运动到最低点A时的速度为v3.根据机械能守恒定律得:
$\frac{1}{2}m{v}_{2}^{2}$+mgl(1-sin30°)=$\frac{1}{2}m{v}_{3}^{2}$
解得 v3=$\sqrt{\frac{5}{2}gl}$
在最低点,由牛顿第二定律得:
T-mg=m$\frac{{v}_{3}^{2}}{l}$
解得 T=3.5mg
答:
(1)细线刚拉紧时的速度大小是$\sqrt{2gl}$;
(2)小球运动到最低点A时绳子受到的拉力是3.5mg.
点评 解决本题的关键要把握住细线绷紧前后速度的变化,要注意中学阶段的细线是刚性的,不可伸长,细线绷紧瞬间沿细线方向的速度突然减至零.

练习册系列答案
相关题目
9. 上饶市云碧峰森林公园装有供游人休闲的吊床,吊床用绳子拴在两棵树上等高的位置.某人先坐在吊床上,后躺在吊床上,均处于静止状态.设吊床两端系绳的拉力为F1、吊床对该人的作用力为F2,则( )
上饶市云碧峰森林公园装有供游人休闲的吊床,吊床用绳子拴在两棵树上等高的位置.某人先坐在吊床上,后躺在吊床上,均处于静止状态.设吊床两端系绳的拉力为F1、吊床对该人的作用力为F2,则( )
 上饶市云碧峰森林公园装有供游人休闲的吊床,吊床用绳子拴在两棵树上等高的位置.某人先坐在吊床上,后躺在吊床上,均处于静止状态.设吊床两端系绳的拉力为F1、吊床对该人的作用力为F2,则( )
上饶市云碧峰森林公园装有供游人休闲的吊床,吊床用绳子拴在两棵树上等高的位置.某人先坐在吊床上,后躺在吊床上,均处于静止状态.设吊床两端系绳的拉力为F1、吊床对该人的作用力为F2,则( )| A. | 坐着比躺着时F1大 | B. | 躺着比坐着时F1大 | ||
| C. | 坐着比躺着时F2大 | D. | 躺着与坐着时F2一样大 |
6. 如图所示,通过定滑轮悬挂两个质量为m1和m2的物体,其中m1>m2,不计绳子质量、绳子与滑轮间的摩擦等,当m1向下运动一段时间距离的过程中,下列说法正确的是( )
如图所示,通过定滑轮悬挂两个质量为m1和m2的物体,其中m1>m2,不计绳子质量、绳子与滑轮间的摩擦等,当m1向下运动一段时间距离的过程中,下列说法正确的是( )
 如图所示,通过定滑轮悬挂两个质量为m1和m2的物体,其中m1>m2,不计绳子质量、绳子与滑轮间的摩擦等,当m1向下运动一段时间距离的过程中,下列说法正确的是( )
如图所示,通过定滑轮悬挂两个质量为m1和m2的物体,其中m1>m2,不计绳子质量、绳子与滑轮间的摩擦等,当m1向下运动一段时间距离的过程中,下列说法正确的是( )| A. | m1势能的减少量等于m1动能的增加量 | |
| B. | m1势能的减少量等于m2势能的增加量 | |
| C. | m1势能的减少量等于m1与m2两者动能的增加量 | |
| D. | m1机械能的减少量等于m2机械能的增加量 |
3. 某学生做观察电磁感应现象的实验,错将电流表、线圈A和B、滑动变阻器、蓄电池、电键用导线连接成如图7的实验电路,则下列说法中正确的是( )
某学生做观察电磁感应现象的实验,错将电流表、线圈A和B、滑动变阻器、蓄电池、电键用导线连接成如图7的实验电路,则下列说法中正确的是( )
 某学生做观察电磁感应现象的实验,错将电流表、线圈A和B、滑动变阻器、蓄电池、电键用导线连接成如图7的实验电路,则下列说法中正确的是( )
某学生做观察电磁感应现象的实验,错将电流表、线圈A和B、滑动变阻器、蓄电池、电键用导线连接成如图7的实验电路,则下列说法中正确的是( )| A. | 接通和断开电键时,电流表的指针都不发生偏转 | |
| B. | 接通和断开电键时,电流表指针偏转方向一正一反 | |
| C. | 电键接通,分别向左和向右移动滑线变阻器滑片时,电流表指针偏转方向相同 | |
| D. | 电键接通,分别向左和向右移动滑线变阻器滑片时,电流表指针都不发生偏转 |
10. 位于A、B处的两个带有不等量负电的点电荷在平面内等差等势面的分布如图所示,图中实线表示等势线,a,b,c,d,e,f是分布在等势面上的点,则( )
位于A、B处的两个带有不等量负电的点电荷在平面内等差等势面的分布如图所示,图中实线表示等势线,a,b,c,d,e,f是分布在等势面上的点,则( )
 位于A、B处的两个带有不等量负电的点电荷在平面内等差等势面的分布如图所示,图中实线表示等势线,a,b,c,d,e,f是分布在等势面上的点,则( )
位于A、B处的两个带有不等量负电的点电荷在平面内等差等势面的分布如图所示,图中实线表示等势线,a,b,c,d,e,f是分布在等势面上的点,则( )| A. | a点和b点的电场强度相同 | |
| B. | 正电荷从c点移到d点,电场力做正功 | |
| C. | 负电荷从a点移到c点,电场力做正功 | |
| D. | 正电荷从e点沿图中虚线移到f点电势能先减小后增大 |
7. 如图所示,a、b、c为静电场中一条直线上的三点,b为ac中点.a、c两点的电势分别为φa=6V、φc=2V.下列说法中正确的是( )
如图所示,a、b、c为静电场中一条直线上的三点,b为ac中点.a、c两点的电势分别为φa=6V、φc=2V.下列说法中正确的是( )
 如图所示,a、b、c为静电场中一条直线上的三点,b为ac中点.a、c两点的电势分别为φa=6V、φc=2V.下列说法中正确的是( )
如图所示,a、b、c为静电场中一条直线上的三点,b为ac中点.a、c两点的电势分别为φa=6V、φc=2V.下列说法中正确的是( )| A. | ab和bc之间的电势差大小关系一定为Uab=Ubc | |
| B. | 电场强度的方向一定为由a指向b | |
| C. | 正电荷在a点的电势能一定大于在c点的电势能 | |
| D. | a点的电场强度一定大于c点的电场强度 |
 如图所示,一个质量为m=2×10-15kg,电荷量为q=+3×10-10c的带电粒子(重力忽略不计),从静止开始经U1=90V电压加速后,由中点水平进入两水平平行金属板间的偏转电场,偏转电场的电压U2=70V,金属板长L=30$\sqrt{3}$cm,板间距离d=35cm.求
如图所示,一个质量为m=2×10-15kg,电荷量为q=+3×10-10c的带电粒子(重力忽略不计),从静止开始经U1=90V电压加速后,由中点水平进入两水平平行金属板间的偏转电场,偏转电场的电压U2=70V,金属板长L=30$\sqrt{3}$cm,板间距离d=35cm.求