题目内容
15. 质量m=0.1kg的小球套在轻杆上,杆固定在墙上;劲度系数为k=200N/m弹簧的一段固定在墙壁上,另一端与小球相连,当轻杆和水平面的夹角是37°时,小球恰好处于静止状态,此时弹簧的形变量为0.01m.小球和杆的动摩擦因数可能为( )
质量m=0.1kg的小球套在轻杆上,杆固定在墙上;劲度系数为k=200N/m弹簧的一段固定在墙壁上,另一端与小球相连,当轻杆和水平面的夹角是37°时,小球恰好处于静止状态,此时弹簧的形变量为0.01m.小球和杆的动摩擦因数可能为( )| A. | 0.25 | B. | 0.4 | C. | 0.5 | D. | 0.75 |
分析 先根据胡克定律求出弹簧的弹力,然后分两种情况分别讨论,对小球进行受力分析,结合共点力的平衡条件即可求出.
解答 解:弹簧的形变量为0.1m,则弹簧的弹力:F=kx=200×0.01=2N

若弹簧处于拉长状态,则受力如图1,得:N=Fsin37°-mgcos37°=2×0.6-1×0.8=0.4N;f=F•cos37°+mgsin37°=2×0.8+1×0.6=2.2N
由于摩擦力比支持力还大,所以这显然是不可能的.
若弹簧处于压缩状态,则受力如图2,得:N=Fsin37°+mgcos37°=2×0.6+1×0.8=2N;f=F•cos37°-mgsin37°=2×0.8-1×0.6=1N
由f=μN.
$μ=\frac{f}{N}=\frac{1}{2}=0.5$
故选:C
点评 共同考查共点力的平衡,要注意的是题目没有说明弹簧是伸长还是压缩,所以要按照两种可能的情况进行讨论,不能由疏漏.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
5. 如图所示,某理想变压器的原副线圈的匝数均可调节,原线圈两端的电压为一最大值不变的正弦交流电,在其他条件不变的情况下,为了使变压器输入功率增大,可使( )
如图所示,某理想变压器的原副线圈的匝数均可调节,原线圈两端的电压为一最大值不变的正弦交流电,在其他条件不变的情况下,为了使变压器输入功率增大,可使( )
 如图所示,某理想变压器的原副线圈的匝数均可调节,原线圈两端的电压为一最大值不变的正弦交流电,在其他条件不变的情况下,为了使变压器输入功率增大,可使( )
如图所示,某理想变压器的原副线圈的匝数均可调节,原线圈两端的电压为一最大值不变的正弦交流电,在其他条件不变的情况下,为了使变压器输入功率增大,可使( )| A. | 原线圈匝数增加 | B. | 负载电阻的阻值增大 | ||
| C. | 副线圈匝数增加 | D. | 负载电阻的阻值减小 |
6. 如图,在一光滑的水平面上,有质量相同的三个小球A、B、C,其中B、C静止,中间连有一轻弹簧,弹簧处于自由伸长状态,现小球A以速度v与小球B正碰并粘在一起,碰撞时间极短,则在此碰撞过程中( )
如图,在一光滑的水平面上,有质量相同的三个小球A、B、C,其中B、C静止,中间连有一轻弹簧,弹簧处于自由伸长状态,现小球A以速度v与小球B正碰并粘在一起,碰撞时间极短,则在此碰撞过程中( )
 如图,在一光滑的水平面上,有质量相同的三个小球A、B、C,其中B、C静止,中间连有一轻弹簧,弹簧处于自由伸长状态,现小球A以速度v与小球B正碰并粘在一起,碰撞时间极短,则在此碰撞过程中( )
如图,在一光滑的水平面上,有质量相同的三个小球A、B、C,其中B、C静止,中间连有一轻弹簧,弹簧处于自由伸长状态,现小球A以速度v与小球B正碰并粘在一起,碰撞时间极短,则在此碰撞过程中( )| A. | A、B的速度变为$\frac{v}{3}$,C的速度仍为0 | B. | A、B、C的速度均为$\frac{v}{3}$ | ||
| C. | A、B的速度变为$\frac{v}{2}$,C的速度仍为0 | D. | A、B、C的速度均为$\frac{v}{2}$ |
3. 人站在岸上通过定滑轮用绳牵引低处的小船,如图所示,若水的阻力恒定不变,则在船匀速靠岸的过程中,下列说法正确的是( )
人站在岸上通过定滑轮用绳牵引低处的小船,如图所示,若水的阻力恒定不变,则在船匀速靠岸的过程中,下列说法正确的是( )
 人站在岸上通过定滑轮用绳牵引低处的小船,如图所示,若水的阻力恒定不变,则在船匀速靠岸的过程中,下列说法正确的是( )
人站在岸上通过定滑轮用绳牵引低处的小船,如图所示,若水的阻力恒定不变,则在船匀速靠岸的过程中,下列说法正确的是( )| A. | 人收绳的速度越来越大 | B. | 人收绳的速度越来越慢 | ||
| C. | 船受到的浮力保持减小 | D. | 船受到的浮力不断不变 |
1.电阻A、B的伏安曲线如图所示,下面说法正确的是( )


| A. | 两电阻串联后的伏安曲线在区域I内,两电阻并联后的伏安曲线在区域II内 | |
| B. | 两电阻串联后的伏安曲线在区域III内,两电阻并联后的伏安曲线在区域I内 | |
| C. | A、B电阻阻值之比为 1:3 | |
| D. | A、B电阻阻值之比为 3:1 |
18.质量为m的跳水运动员,从离水面高h的跳台上以速度v1斜向上跳起,跳起的最大高度为H(离跳台),最后又以速度v2进入水池中,不计空气阻力,则运动员起跳时所做的功是( )
| A. | $\frac{1}{2}$mv12 | B. | mg(H+h) | C. | $\frac{1}{2}$mv12+mgh | D. | $\frac{1}{2}$mv22-mgh |

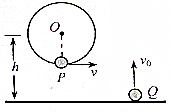 如图所示,小球P固定于圆盘上,小球Q位于地面上,开始时小球P从圆盘的最低点绕圆盘的圆心做匀速圆周运动,同时小球Q以初速度v0=8m/s做竖直上抛运动,已知圆盘的圆心离地面的高h=2.4m,g=10m/s2,在运动过程中发现两小球在同一高度有速度相等的情况存在,问圆盘的半径是多大?
如图所示,小球P固定于圆盘上,小球Q位于地面上,开始时小球P从圆盘的最低点绕圆盘的圆心做匀速圆周运动,同时小球Q以初速度v0=8m/s做竖直上抛运动,已知圆盘的圆心离地面的高h=2.4m,g=10m/s2,在运动过程中发现两小球在同一高度有速度相等的情况存在,问圆盘的半径是多大?