题目内容
15.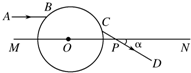 如图所示,一透明球体置于空气中,球半径R=10cm,折射率n=$\sqrt{2}$,MN是一条通过球心的直线,单色细光束AB平行于MN射向球体,B为入射点,AB与MN间距为5$\sqrt{2}$cm,CD为出射光线.
如图所示,一透明球体置于空气中,球半径R=10cm,折射率n=$\sqrt{2}$,MN是一条通过球心的直线,单色细光束AB平行于MN射向球体,B为入射点,AB与MN间距为5$\sqrt{2}$cm,CD为出射光线.(1)求出光从B点传到C点的时间
(2)求CD与MN所成的角α.
分析 (1)画出光路图,由几何知识求入射角,由折射定律求出折射角,再几何关系求出BC距离,由公式v=$\frac{c}{n}$求出光在球体传播速度,即可由t=$\frac{\overline{BC}}{v}$得到光从B点传到C点的时间.
(2)由光路可逆性得到光线射出球体时的折射角,由几何知识求α.
解答  解:(1)画出光路图如图.
解:(1)画出光路图如图.
由几何知识有:sini=$\frac{BE}{BO}$=$\frac{5\sqrt{2}}{10}$=$\frac{\sqrt{2}}{2}$,则i=45°
由n=$\frac{sini}{sinr}$=$\sqrt{2}$得:r=30°
由几何关系可得B到C的距离为:s=2Rcos30°=$\sqrt{3}$R
光在球体传播速度为:v=$\frac{c}{n}$
故光从B点传到C点的时间为:t=$\frac{s}{v}$=$\frac{\sqrt{3}nR}{c}$=$\frac{\sqrt{3}×\sqrt{2}×0.1}{3×1{0}^{8}}$=$\frac{\sqrt{6}}{3}×1{0}^{-9}$s
(2)根据光路可逆原理得知光线射出球体时的折射角等于i=45°
由几何关系得:∠BOC=120°,∠BOE=45°,∠COP=180°-∠BOC-∠BOE=15°
故α=i-∠COP=45°-15°=30°
答:(1)光从B点传到C点的时间是$\frac{\sqrt{6}}{3}×1{0}^{-9}$s.
(2)CD与MN所成的角α是30°.
点评 本题考查了光的折射定律,正确画出光路图、利用几何知识求入射角和折射角是解决本题的关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
4. 如图,在电场中有a,b两点,试比较a,b两点场强的大小Ea、Eb;引入一个点电荷,比较在a,b两处受到的电场力Fa,Fb,则( )
如图,在电场中有a,b两点,试比较a,b两点场强的大小Ea、Eb;引入一个点电荷,比较在a,b两处受到的电场力Fa,Fb,则( )
 如图,在电场中有a,b两点,试比较a,b两点场强的大小Ea、Eb;引入一个点电荷,比较在a,b两处受到的电场力Fa,Fb,则( )
如图,在电场中有a,b两点,试比较a,b两点场强的大小Ea、Eb;引入一个点电荷,比较在a,b两处受到的电场力Fa,Fb,则( )| A. | Ea>Eb;Fa>Fb | B. | Ea>Eb;Fa<Fb | C. | Ea<Eb;Fa<Fb | D. | Ea=Eb;Fa=Fb |
10. 橡皮筋也像弹簧一样,在弹性限度内,伸长量x与弹力F成正比,即F=kx,k的值与橡皮筋未受到拉力时的长度L、横截面积S有关,理论与实践都表明k=Y $\frac{S}{L}$,其中Y是一个由材料决定的常数,材料力学上称之为杨氏模量.
橡皮筋也像弹簧一样,在弹性限度内,伸长量x与弹力F成正比,即F=kx,k的值与橡皮筋未受到拉力时的长度L、横截面积S有关,理论与实践都表明k=Y $\frac{S}{L}$,其中Y是一个由材料决定的常数,材料力学上称之为杨氏模量.
(1)在国际单位制中,杨氏模量Y的单位应该是D
A.N B.m C.N/m D.Pa
(2)有一段横截面是圆形的橡皮筋,应用如图所示的实验装置可以测量出它的杨氏模量Y的值.首先利用测量工具a测得橡皮筋的长度L=20.00cm,利用测量工具b测得橡皮筋未受到拉力时的直径D=4.000mm,那么测量工具a应该是毫米刻度尺,测量工具b应该是螺旋测微器.
(3)下面的表格是橡皮筋受到的拉力F与伸长量x的实验记录.
可求得该橡皮筋的劲度系数k=3.1×102N/m.
(4)这种橡皮筋的Y值等于5×106 Pa.
 橡皮筋也像弹簧一样,在弹性限度内,伸长量x与弹力F成正比,即F=kx,k的值与橡皮筋未受到拉力时的长度L、横截面积S有关,理论与实践都表明k=Y $\frac{S}{L}$,其中Y是一个由材料决定的常数,材料力学上称之为杨氏模量.
橡皮筋也像弹簧一样,在弹性限度内,伸长量x与弹力F成正比,即F=kx,k的值与橡皮筋未受到拉力时的长度L、横截面积S有关,理论与实践都表明k=Y $\frac{S}{L}$,其中Y是一个由材料决定的常数,材料力学上称之为杨氏模量.(1)在国际单位制中,杨氏模量Y的单位应该是D
A.N B.m C.N/m D.Pa
(2)有一段横截面是圆形的橡皮筋,应用如图所示的实验装置可以测量出它的杨氏模量Y的值.首先利用测量工具a测得橡皮筋的长度L=20.00cm,利用测量工具b测得橡皮筋未受到拉力时的直径D=4.000mm,那么测量工具a应该是毫米刻度尺,测量工具b应该是螺旋测微器.
(3)下面的表格是橡皮筋受到的拉力F与伸长量x的实验记录.
| 拉力F/N | 5 | 10 | 15 | 20 | 25 |
| 伸长量x/cm | 1.6 | 3.2 | 4.7 | 6.4 | 8.0 |
(4)这种橡皮筋的Y值等于5×106 Pa.
4. 如图所示是发电厂通过升压变压器进行高压输电,接近用户端时再通过降压变压器降压给用户供电的示意图(图中变压器均可视为理想变压器,图中电表均为理想交流电表).设发电厂输出的电压一定,两条输电线总电阻用R0表示,变阻器R相当于用户用电器的总电阻.当用电器增加时,相当于R变小,则当用电进入高峰时( )
如图所示是发电厂通过升压变压器进行高压输电,接近用户端时再通过降压变压器降压给用户供电的示意图(图中变压器均可视为理想变压器,图中电表均为理想交流电表).设发电厂输出的电压一定,两条输电线总电阻用R0表示,变阻器R相当于用户用电器的总电阻.当用电器增加时,相当于R变小,则当用电进入高峰时( )
 如图所示是发电厂通过升压变压器进行高压输电,接近用户端时再通过降压变压器降压给用户供电的示意图(图中变压器均可视为理想变压器,图中电表均为理想交流电表).设发电厂输出的电压一定,两条输电线总电阻用R0表示,变阻器R相当于用户用电器的总电阻.当用电器增加时,相当于R变小,则当用电进入高峰时( )
如图所示是发电厂通过升压变压器进行高压输电,接近用户端时再通过降压变压器降压给用户供电的示意图(图中变压器均可视为理想变压器,图中电表均为理想交流电表).设发电厂输出的电压一定,两条输电线总电阻用R0表示,变阻器R相当于用户用电器的总电阻.当用电器增加时,相当于R变小,则当用电进入高峰时( )| A. | 电压表V1、V2的读数均不变,电流表A2的读数增大,电流表A1的读数减小 | |
| B. | 电压表V3、V4的读数均减小,电流表A2的读数增大,电流表A3的读数减小 | |
| C. | 电流表V2、V3的读数之差与电流表A2 的读数的比值不变 | |
| D. | 发电厂的输出功率增大 |


 如图所示,一正方形金属线框边长为a,从磁场上方某一高度、自由下落,磁场边界宽为3a,则线框从进入磁场到完全离开磁场的过程中,线框速度随时间变化的图象可能是下图中( )
如图所示,一正方形金属线框边长为a,从磁场上方某一高度、自由下落,磁场边界宽为3a,则线框从进入磁场到完全离开磁场的过程中,线框速度随时间变化的图象可能是下图中( )


