题目内容
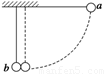
如图所示,用两根长度都为L的细绳,把质量相等、大小相同的a、b两球悬挂于同一高度,静止时两球恰好接触,现把a球拉到细绳处于水平位置,然后由静止释放,当a球摆到最低点与b球相碰后,b球上摆的最大高度不可能为( )
A.L
B. 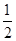 L
C.
L
C. 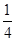 L
D.
L
D. 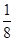 L
L
【答案】
D
【解析】
试题分析:碰撞后系统动能不能超过碰前总动能,动能损失有一个范围.即两球发生完全弹性碰撞,系统没有动能损失时,b球上摆的高度最大,此时两球交换速度,b球上升到原a球所在的高度,选项A正确;当两球发生完全非弹性碰撞(碰后两球粘在一起),系统动能损失最大时,b球上摆的高度最小,对a球用机械能守恒定律得mgL=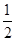 mv
mv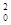 ,由动量守恒定律有:mv0=2mv.a、b球以共同速度一起上摆,
,由动量守恒定律有:mv0=2mv.a、b球以共同速度一起上摆,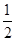 (2m)v2=2mgh,解以上两式得h=
(2m)v2=2mgh,解以上两式得h=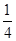 L.选项A、B、C可能,只有选项D不可能.
L.选项A、B、C可能,只有选项D不可能.
考点:动量守恒 能量守恒
点评:本题关键抓住系统动量守恒这一条件列方程求解,解答碰撞类问题时要注意应用动量守恒结合能量的观点求解.动量守恒的前提下,动能是不能增加的。

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
 如图所示,用两根长度都为l的细线悬挂一个小球A,两悬挂点等高,线与水平天花板间的夹角都是α,使球A在垂直于纸面的平面内做小幅度的摆动,当A经过平衡位置的瞬间,另一小球B从A球的正上方自由下落,若B球恰能击中A球,求B球开始下落时离A球振动平衡位置的高度.
如图所示,用两根长度都为l的细线悬挂一个小球A,两悬挂点等高,线与水平天花板间的夹角都是α,使球A在垂直于纸面的平面内做小幅度的摆动,当A经过平衡位置的瞬间,另一小球B从A球的正上方自由下落,若B球恰能击中A球,求B球开始下落时离A球振动平衡位置的高度. 如图所示,用两根长度都为L的细绳,把质量相等大小相同的a、b两球悬挂于同一高度,静止时两球恰好接触,现把a球拉到细绳处于水平位置,然后由静止释放,当a球摆到最低点与b球相碰后,b球上摆的最大高度可能为( )
如图所示,用两根长度都为L的细绳,把质量相等大小相同的a、b两球悬挂于同一高度,静止时两球恰好接触,现把a球拉到细绳处于水平位置,然后由静止释放,当a球摆到最低点与b球相碰后,b球上摆的最大高度可能为( )

