题目内容
匀强磁场分布在半径为R的圆内，磁感应强度为B，CD是圆的直径．质量为m、电量为q的带正电粒子，由静止开始经加速电场加速后，沿着与直径CD平行且相距0.6R的直线从A点进入磁场，如图所示．若带电粒子在磁场中运动的时间是| πm | 2qB |
分析：根据匀速圆周运动的周期公式，结合几何关系与动量公式，即可求解．
解答：
解：带电粒子在磁场中做匀速圆周运动的周期是T=
；
粒子在磁场中运动的时间是t=
=
如图所示，粒子从A点进入磁场后，从E点射出．O为磁场圆的圆心，
设∠AOC=α
则sinα=0.6
粒子做圆周运动的圆心是O1点，设半径O1A=r，
O1A⊥CD，∠COO1=45°．
由图可知
=
r=R（sinα+cosα）=1.4R
粒子做圆周运动的半径r=
，
解得粒子动量大小P=mv=1.4qRB，
解得加速电压U=
=
答：加速电场的加速电压
．
解：带电粒子在磁场中做匀速圆周运动的周期是T=| 2πm |
| qB |
粒子在磁场中运动的时间是t=
| πm |
| 2qB |
| T |
| 4 |
如图所示，粒子从A点进入磁场后，从E点射出．O为磁场圆的圆心，
设∠AOC=α
则sinα=0.6
粒子做圆周运动的圆心是O1点，设半径O1A=r，
O1A⊥CD，∠COO1=45°．
由图可知
| R |
| sin45° |
| r |
| sin(45°+α) |
r=R（sinα+cosα）=1.4R
粒子做圆周运动的半径r=
| mv |
| qB |
解得粒子动量大小P=mv=1.4qRB，
解得加速电压U=
| P2 |
| 2mq |
| 0.98qB2R2 |
| m |
答：加速电场的加速电压
| 0.98qB2R2 |
| m |
点评：考查粒子在磁场的做圆弧运动，在洛伦兹力提供向心力作用下，掌握周期与半径公式，理解几何关系的应用，并知道动量的表达式．
练习册系列答案
阅读快车系列答案
相关题目
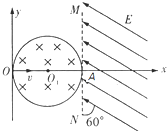如图所示，磁感应强度大小B=1T，方向垂直纸面向里的匀强磁场分布在半径为R=
如图所示，磁感应强度大小B=0.15T，方向垂直纸面向里的匀强磁场分布在半径为R=0.10m的圆形区域内，圆的左端跟y轴相切于直角坐标系的原点O，右端边界MN相切于x轴的A点．MN右侧有方向平行于x轴负方向的匀强电场．置于原点O的粒子源，可沿x轴正方向射出速度v=3.0×106m/s的带正电的粒子流，荷质比q/m=1.0×108c/kg，粒子重力不计．右侧场强大小E=2.0×105V/m．现以过O点并垂直于纸面的直线为轴，将圆形磁场区域按逆时针方向缓慢旋转90°．
。求加速电场的加速电压。
如图所示，磁感应强度大小B=0.15T，方向垂直纸面向里的匀强磁场分布在半径为R=0．10m的圆形区域内，圆的左端跟
轴相切于直角出标系的原点
，右端边界MN相切于
轴的A点。MN右侧有方向平行于
的带正电的粒子流，荷质比
，粒子重力不计。右侧场强大小
。现以过
；
；
为多大？