题目内容
1.有一质量为800kg的小汽车驶上圆弧半径为40m的拱桥.若汽车到达桥顶时的速度为5m/s,取g=10m/s2,求:(1)汽车对桥的压力.
(2)为了行驶安全,小汽车的速度不能超过多少?
分析 (1)在桥顶,小汽车靠重力和支持力的合力提供向心力,结合牛顿第二定律求出支持力的大小,从而得出汽车队桥顶的压力.
(2)当支持力为零时,汽车的速度最大,结合牛顿第二定律求出小汽车在桥顶的最大速度.
解答 解:(1)根据牛顿第二定律得:$mg-N=m\frac{{v}^{2}}{R}$,
解得支持力为:N=$mg-m\frac{{v}^{2}}{R}=8000-800×\frac{25}{40}$N=7500N.
根据牛顿第三定律知,汽车对桥顶的压力为7500N.
(2)根据mg=m$\frac{{v}^{2}}{R}$得汽车在桥顶的最大速度为:
v=$\sqrt{gR}=\sqrt{10×40}$ms/=20m/s.
答:(1)汽车对桥的压力为7500N.
(2)为了行驶安全,小汽车的速度不能超过20m/s.
点评 解决本题的关键知道汽车在最高点向心力的来源,抓住临界状态,结合牛顿第二定律进行求解,难度不大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13. 如图所示,人用绳子通过动滑轮拉A,A穿在光滑的竖直杆上,若人匀速向下拉绳使物体A沿杆向上运动,则物体A作何运动( )
如图所示,人用绳子通过动滑轮拉A,A穿在光滑的竖直杆上,若人匀速向下拉绳使物体A沿杆向上运动,则物体A作何运动( )
 如图所示,人用绳子通过动滑轮拉A,A穿在光滑的竖直杆上,若人匀速向下拉绳使物体A沿杆向上运动,则物体A作何运动( )
如图所示,人用绳子通过动滑轮拉A,A穿在光滑的竖直杆上,若人匀速向下拉绳使物体A沿杆向上运动,则物体A作何运动( )| A. | 匀速 | B. | 加速 | C. | 减速 | D. | 无法确定 |
10.下列关于产生感应电流的说法正确的是( )
| A. | 一段导体在磁场中运动时,能产生感应电流 | |
| B. | 当闭合电路的部分导体沿磁感线运动时,能产生感应电流 | |
| C. | 当闭合电路的部分导体做切割磁感线运动时,能产生感应电流 | |
| D. | 闭合电路的导体在磁场中不运动就不能产生感应电流 |
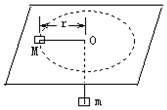 如图所示,细绳一端系着质量M=2kg的物体,静止在水平面,另一端通过光滑小孔吊着质量m=0.3kg的物体,M的中点与圆孔距离为0.2m,并知M和水平面的最大静摩擦力为7N,现使此平面绕中心轴转动,问角速度ω在什么范围内m会处于静止状态?g取10m/s2.
如图所示,细绳一端系着质量M=2kg的物体,静止在水平面,另一端通过光滑小孔吊着质量m=0.3kg的物体,M的中点与圆孔距离为0.2m,并知M和水平面的最大静摩擦力为7N,现使此平面绕中心轴转动,问角速度ω在什么范围内m会处于静止状态?g取10m/s2. 如图所示,在米尺的一端钻一个小孔,使小孔恰能穿过一根细线,线下端挂一质量为m的小钢球(视为质点).将米尺固定在水平桌面上,使钢球在水平面内做匀速圆周运动,圆心为O,待钢球的运动稳定后,读出钢球到O点的距离r,并用秒表测量出钢球转动n圈用的时间t.则:
如图所示,在米尺的一端钻一个小孔,使小孔恰能穿过一根细线,线下端挂一质量为m的小钢球(视为质点).将米尺固定在水平桌面上,使钢球在水平面内做匀速圆周运动,圆心为O,待钢球的运动稳定后,读出钢球到O点的距离r,并用秒表测量出钢球转动n圈用的时间t.则: 如图所示,装置BO′O可绕竖直轴O′O转动,可视为质点的小球A与两细线连接后分别系于B、C两点,装置静止AB水平,细线AC与竖直方向的夹角θ=37°.已知小球的质量m=1kg,细线AC长l=0.5m,B点距C点的水平距离和竖直距离相等,(重力加速度g取10m/s2,sin37°=$\frac{3}{5}$,cos37°=$\frac{4}{5}$).
如图所示,装置BO′O可绕竖直轴O′O转动,可视为质点的小球A与两细线连接后分别系于B、C两点,装置静止AB水平,细线AC与竖直方向的夹角θ=37°.已知小球的质量m=1kg,细线AC长l=0.5m,B点距C点的水平距离和竖直距离相等,(重力加速度g取10m/s2,sin37°=$\frac{3}{5}$,cos37°=$\frac{4}{5}$). 如图甲所示,水平传送带在电动机带动下保持以速度v0向右运动,传送带长L=10m,t=0时刻,将质量为m=1kg的木块轻放在传送带左端,木块向右运动的速度-时间图象(v-t)如图乙所示.当木块刚运动到传送带最右端时(未滑下传送带),一颗子弹水平向左正对射入木块并穿出,木块速度变为v=3m/s,方向水平向左,以后每隔时间△t=1s就有一颗相同的子弹向左射向木块.设子弹与木块的作用时间极短,且每次子弹穿出后木块的速度都变为方向水平向左大小为v=3m/s,木块长度比传送带长度小得多,可忽略不计,子弹穿过木块前后木块质量不变,重力加速度取g=10m/s2.求:
如图甲所示,水平传送带在电动机带动下保持以速度v0向右运动,传送带长L=10m,t=0时刻,将质量为m=1kg的木块轻放在传送带左端,木块向右运动的速度-时间图象(v-t)如图乙所示.当木块刚运动到传送带最右端时(未滑下传送带),一颗子弹水平向左正对射入木块并穿出,木块速度变为v=3m/s,方向水平向左,以后每隔时间△t=1s就有一颗相同的子弹向左射向木块.设子弹与木块的作用时间极短,且每次子弹穿出后木块的速度都变为方向水平向左大小为v=3m/s,木块长度比传送带长度小得多,可忽略不计,子弹穿过木块前后木块质量不变,重力加速度取g=10m/s2.求: