��Ŀ����
5�� ����Ϊd������������ڴŸ�Ӧǿ�ȴ�С��ȣ������෴����ǿ�ų�����ͼ��ʾ����MN��ų����Ҳ�߽�ľ���Ҳ����d��ֱ��OO����ų��߽��Լ���MN����ֱ��һ����Ϊm�������Ϊe�ĵ��Ӵ�O�����ٶ�v0����ų����ٶȷ�����ֱ��OO���45��ǣ��Ÿ�Ӧǿ��B�Ĵ�С��ͬ�������˶��켣Ҳ��ͬ��
����Ϊd������������ڴŸ�Ӧǿ�ȴ�С��ȣ������෴����ǿ�ų�����ͼ��ʾ����MN��ų����Ҳ�߽�ľ���Ҳ����d��ֱ��OO����ų��߽��Լ���MN����ֱ��һ����Ϊm�������Ϊe�ĵ��Ӵ�O�����ٶ�v0����ų����ٶȷ�����ֱ��OO���45��ǣ��Ÿ�Ӧǿ��B�Ĵ�С��ͬ�������˶��켣Ҳ��ͬ����1��Ҫʹ�����ܴ���MN�ϴŸ�Ӧǿ��B�Ĵ�СӦ�����������
��2�����Ӵ�����MN�ϵķ�Χ�Ƕ��٣�
���� ��1�������ڴų���������Բ���˶������������ṩ������������ţ�ٵڶ����ɹ�ʽ�������⣮
��2�����ݵ��ӵ��˶����̣��ó������ڴų����˶��ĶԳ���������ų�ʱ���ٶȵķ���Ȼ��ȷ�����Ӵ�����MN�ϵķ�Χ��
��� �⣺��1�������ڴų���������Բ���˶���
����ǡ�ô�MN��ʱ�������˶��켣��ͼ��ʾ��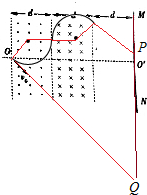
�ɼ���֪ʶ��֪��r+rcos45��=d����ã�r=��2-$\sqrt{2}$��d��
�����ڴų���������Բ���˶������������ṩ��������
��ţ�ٵڶ����ɵã�ev0B=m$\frac{{v}_{0}^{2}}{r}$��
��ã�r=$\frac{m{v}_{0}}{eB}$��B=$\frac{m{v}_{0}}{��2-\sqrt{2}��ed}$��
��r=$\frac{m{v}_{0}}{eB}$��֪��BԽС��rԽ��
���Ӵ���MN�ϵ������ǣ�B��$\frac{m{v}_{0}}{��2-\sqrt{2}��ed}$��
��2����ͼʾ��֪������ǡ������ų�ʱ��O��P=rsin45��+r-$\frac{d}{tan45��}$-r��1-sin45�㣩=��3-2$\sqrt{2}$��d��
���ų��ĴŸ�Ӧǿ�ȷdz�С�������ӽ���������ֱ���˶���������ĵ㣺O��Q=3d•tan45��=3d
���ԣ����Ӵ�����MN�ϵķ�Χ�ǣ���O�����ϵ�O��ľ���С�ڣ�3-2$\sqrt{2}$��d����O�����µ�O��ľ���С��3d��Χ�ڣ�
�𣺣�1��Ҫʹ�����ܴ���MN�ϴŸ�Ӧǿ��B�Ĵ�СӦ����B��$\frac{m{v}_{0}}{��2-\sqrt{2}��ed}$��
��2�����Ӵ�����MN�ϵķ�Χ����O�����ϵ�O��ľ���С�ڣ�3-2$\sqrt{2}$��d����O�����µ�O��ľ���С��3d��Χ�ڣ�
���� ���⿼���˵����ڴų��е��˶��������ڴų���������Բ���˶������������ṩ������������������ӵ��˶����̡�Ӧ��ţ�ٵڶ����ɼ�����ȷ���⣬����ʱע�⼸��֪ʶ��Ӧ�ã�

| A�� | �ʵ�һ�������ȼ���ֱ���˶� | |
| B�� | �ʵ�ij��ٶ�����ٶȷֱ�Ϊ4m/s��2m/s2 | |
| C�� | �ʵ�ij��ٶ�����ٶȷֱ�Ϊ4m/s��4m/s2 | |
| D�� | �ʵ��ڵ�2��ĩ���ٶ�Ϊ16m/s |

| A�� | mgsin�� | B�� | mgcos�� | C�� | $\frac{mg}{cos��}$ | D�� | mgtan�� |
 ��ͼ��ʾΪ����ǧ�ﶥ��ʾ��ͼ��ǧ�ﶥ��Ҫ�����OA��OB��ƽ̨��ɣ�������������ǧ�ﶥƽ̨����ѹ��Ϊ F��������ƽ̨����������OA���ܵ����Ĵ�С�ǣ�������
��ͼ��ʾΪ����ǧ�ﶥ��ʾ��ͼ��ǧ�ﶥ��Ҫ�����OA��OB��ƽ̨��ɣ�������������ǧ�ﶥƽ̨����ѹ��Ϊ F��������ƽ̨����������OA���ܵ����Ĵ�С�ǣ�������| A�� | Ftg�� | B�� | Fctg�� | C�� | Fsin�� | D�� | $\frac{F}{sin��}$ |
 ��ͼ��ʾ�ĵ�·�У�A��BΪ��ֱ���õ�һ��ƽ�н����幹�ɵĵ�������B������һ��Եϸ������һ����С��С��ֹʱ������B��н�Ϊ�ȣ�DΪ��������ܣ�ֻ���������ڶ������д�a����b�������S�DZպϵģ������������и���������нǦȱ��ֲ�����ǣ�������
��ͼ��ʾ�ĵ�·�У�A��BΪ��ֱ���õ�һ��ƽ�н����幹�ɵĵ�������B������һ��Եϸ������һ����С��С��ֹʱ������B��н�Ϊ�ȣ�DΪ��������ܣ�ֻ���������ڶ������д�a����b�������S�DZպϵģ������������и���������нǦȱ��ֲ�����ǣ�������| A�� | ��A������ƽ��һС�ξ��� | B�� | ��A������ƽ��һС�ξ��� | ||
| C�� | �����������Ļ�ƬP��C�˻��� | D�� | �Ͽ����S |
| A�� | �����A�������ƣ���ô�͵��䵽B��ʱ�պ��ٶ���ȻΪ�� | |
| B�� | �����A�������ƣ���ô�͵��䵽B��ʱ�պ��ٶȴ����� | |
| C�� | �����B�������ƣ���ô�͵��䵽B��ʱ�պ��ٶ���ȻΪ�� | |
| D�� | �����B�������ƣ���ô�͵����䵽B��֮ǰ�ͷ����˶� |
| A�� | �糡��ij��ĵ糡ǿ�� E=$\frac{U}{d}$ | B�� | �Ÿ�Ӧǿ��B=$\frac{F}{IL}$ | ||
| C�� | ����R=$\frac{U}{I}$ | D�� | �糡ǿ��E=k$\frac{Q}{{r}^{2}}$ |

| A�� | ��ʱ�����ĵ糡ǿ��E=$\frac{U}{d}$ | |
| B�� | �͵δ������Ϊ$\frac{mg}{Ud}$ | |
| C�� | ��С������ѹ���͵ν��������� | |
| D�� | ������N���»����ƶ�һС�ξ��룬�͵ν������˶� |
 ��ͼ������Ϊm��С��������Ϊ�ʵ㣩����Ƕ�Ϊ���Ļ�������ֱ�������ٻ��£���֪С�������������ݵ�֧������Ħ���������ã���
��ͼ������Ϊm��С��������Ϊ�ʵ㣩����Ƕ�Ϊ���Ļ�������ֱ�������ٻ��£���֪С�������������ݵ�֧������Ħ���������ã���