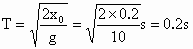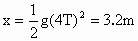题目内容
屋檐每隔一定时间滴下一滴水,当第5滴正欲滴下时,第1滴刚好落到地面,而第3滴与第2滴分别位于高1m的窗子的上、下沿,如图所示,问:

(1)此屋檐离地面多高?
(2)滴水的时间间隔是多少?
答案:3.2m;0.2s
解析:
解析:
|
由图所示,如果将这 5滴水的运动等效为一滴水的自由落体,并且将这一滴水运动的全过程分成时间相等的4段,设时间间隔为T,则这一滴水在0时刻,Ts末、2Ts末、3Ts末、4Ts末所处的位置,分别对应图示第5滴水、第4滴水、第3滴水、第2滴水、第1滴水所处的位置,据此可作出解答.解法一:利用基本规律求解. (1) 设屋檐离地面高为x,滴水间隔为T.由 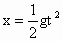 得: 得:
第 2滴水的位移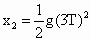 ,① ,①
第 3滴水的位移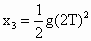 .② .②
又因为 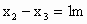 ,③ ,③
所以联立①②③三式,解得 T=0.2s.(2) 屋檐高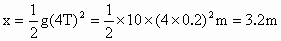 . .
解法二:用比例法求解. (1) 由于初速为零的匀加速直线运动从开始运动起,在连续相等的时间间隔内的位移比为1∶3∶5∶7…∶(2n-1),据此令相邻两水滴之间的间距从上到下依次是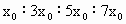 . .
显然,窗高为 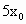 ,即 ,即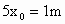 ,得 ,得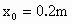 . .
屋檐总高 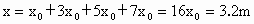 . .
(2) 由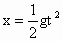 知,滴水时间间隔为 知,滴水时间间隔为
解法Ⅲ:用平均速度求解. (1) 设滴水间隔为T,则雨滴经过窗子过程中的平均速度为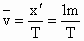 . .
由 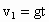 知,雨滴下落2.5T时的速度为 知,雨滴下落2.5T时的速度为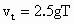 . .
由于 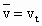 ,故有 ,故有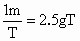 ,解得T=0.2s ,解得T=0.2s
(2) 对于初速为零的匀加速直线运动的规律和有关推论,同样适用于自由落体运动. |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目