题目内容
7.某学校实验小组欲测定正方体木块与长木板之间的动摩擦因数μ,采用如图甲所示的装置,图中长木板水平固定,所用的交流电频率为50Hz.
(1)实验开始之前某同学用20分度游标卡尺测得正方体边长,读数如图乙所示,则正方体的边长为9.015cm.
(2)如图丙所示为该组同学实验中得到的一条纸带的一部分,0,1,2,3,4,5,6为计数点,相邻两计数点间还有4个计时点未画出.从纸带上测出x1=3.20cm,x2=4.52cm,x5=8.42cm,x6=9.70cm,则木块的加速度大小a=1.3 m/s2(保留两位有效数字).
(3)该组同学用天平测得木块的质量为M,砝码盘和砝码的总质量为m,则木块与长木板间动摩擦因数的表达式为μ=$\frac{{mg-({M+m})a}}{Mg}$(重力加速度为g,木块的加速度为a).由于本实验存在系统误差,故动摩擦因数μ的测量值大于(填“大于”、“等于”或“小于”)真实值.
分析 (1)游标卡尺主尺与游标尺示数之和是游标卡尺示数.
(2)利用匀变速直线运动的推论:△x=aT2,可计算出打出某点时纸带运动的加速度.
(3)对木块、砝码盘和砝码进行受力分析,运用牛顿第二定律求出木块与长木板间动摩擦因数
解答 解:(1)由图乙所示游标卡尺可知,主尺示数为9.0cm,
游标尺示数为3×0.05mm=0.15mm=0.015cm,游标卡尺示数为9.0cm+0.015cm=9.015cm.
(2)计数点间的时间间隔t=0.02×5=0.1s,由匀变速运动的推论:△x=at2可得,加速度$a=\frac{{{a_1}+{a_2}}}{2}=\frac{{{x_5}-{x_1}+{x_6}-{x_2}}}{{2×4{t^2}}}=\frac{0.0842-0.0320+0.0970-0.0452}{{8×{{0.1}^2}}}=1.3$m/s2;
(3)对木块、砝码盘和砝码系统,由牛顿第二定律得:mg-μMg=(M+m)a,
解得:μ=$\frac{{mg-({M+m})a}}{Mg}$.
由实验测得的阻力为系统所受的总阻力,比木块受到的滑动摩擦力大,故μ的测量值偏大.
故答案为:(1)9.015 (2)1.3 (3)$\frac{{mg-({M+m})a}}{Mg}$,大于
点评 本题主要考查了利用牛顿第二定律测定木块与长木板之间的动摩擦因数的设计试验问题,属于中档题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
2. 如图所示,A、B为平行板电容器的金属板,G为静电计,开始时开关S闭合,静电计指针张开一定角度.下述结论正确的是( )
如图所示,A、B为平行板电容器的金属板,G为静电计,开始时开关S闭合,静电计指针张开一定角度.下述结论正确的是( )
 如图所示,A、B为平行板电容器的金属板,G为静电计,开始时开关S闭合,静电计指针张开一定角度.下述结论正确的是( )
如图所示,A、B为平行板电容器的金属板,G为静电计,开始时开关S闭合,静电计指针张开一定角度.下述结论正确的是( )| A. | 若保持开关S闭合,将A、B两极板靠近些,指针张开角度将变小 | |
| B. | 若保持开关S闭合,将A、B两极板正对面积变小些,指针张开角度将不变 | |
| C. | 若断开开关S后,将A、B两极板靠近些,指针张开角度将变小 | |
| D. | 若断开开关S后,将A、B两极板正对面积变小些,指针张开角度将变大 |
 如图所示,一截面为直角三角形的玻璃棱镜ABC,∠A=30°.一条光线以45°的入射角从AC边上的D点射入棱镜,光线最终垂直BC边射出.
如图所示,一截面为直角三角形的玻璃棱镜ABC,∠A=30°.一条光线以45°的入射角从AC边上的D点射入棱镜,光线最终垂直BC边射出.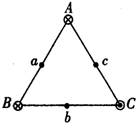 正三角形ABC的三个顶点处分别有垂直于三角形平面的无限长直导线,导线中通有恒定电流,方向如图所示,a、b、c三点分别是正三角形三边的中点,若A、B、C三处导线中的电流分别为I、2I、3I,已知无限长直导线在其周围某一点产生的磁场磁感应强度B的大小与电流成正比,与电流到这一点的距离成反比,即B=k$\frac{I}{r}$,则a、b、c三点的磁感应强度大小关系为( )
正三角形ABC的三个顶点处分别有垂直于三角形平面的无限长直导线,导线中通有恒定电流,方向如图所示,a、b、c三点分别是正三角形三边的中点,若A、B、C三处导线中的电流分别为I、2I、3I,已知无限长直导线在其周围某一点产生的磁场磁感应强度B的大小与电流成正比,与电流到这一点的距离成反比,即B=k$\frac{I}{r}$,则a、b、c三点的磁感应强度大小关系为( ) 如图所示,ABCD为一棱镜的横截面,∠A=∠B=90°,∠C=60°,CD面为镀银的反射面,BC边长为L,BC=2AD,一束单色光垂直AB面射入棱镜,从BC面中点P射出后垂直射到与水平方向成30°的光屏MN上,光在真空中速度为c,求:
如图所示,ABCD为一棱镜的横截面,∠A=∠B=90°,∠C=60°,CD面为镀银的反射面,BC边长为L,BC=2AD,一束单色光垂直AB面射入棱镜,从BC面中点P射出后垂直射到与水平方向成30°的光屏MN上,光在真空中速度为c,求: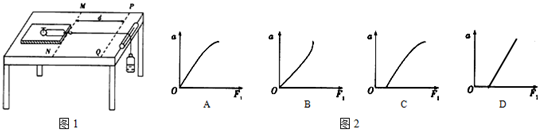
 天文学家观测河外星系大麦哲伦云时,发现了LMCX-3双星系统,它由可见星A和不可见的暗星B构成.两星视为质点,不考虑其他天体的影响,A、B围绕两者连线上的O点做匀速圆周运动,它们之间的距离保持不变,如图所示.引力常量为G,由观测能够得到可见星A的速率v和运行周期T.
天文学家观测河外星系大麦哲伦云时,发现了LMCX-3双星系统,它由可见星A和不可见的暗星B构成.两星视为质点,不考虑其他天体的影响,A、B围绕两者连线上的O点做匀速圆周运动,它们之间的距离保持不变,如图所示.引力常量为G,由观测能够得到可见星A的速率v和运行周期T.